chirp scaling算法实测数据成像

01 Oct 2024

CSA 成像算法仿真

大斜视角

参数与初始化

load("../data/English_Bay_ships/data_1.mat");
c = 299792458;                     %光速
Fs = 32317000;      %采样率                                   
start = 6.5959e-03;         %开窗时间 
Tr = 4.175000000000000e-05;        %脉冲宽度                        
f0 = 5.300000000000000e+09;                    %载频                     
PRF = 1.256980000000000e+03;       %PRF                     
Vr = 7062;                       %雷达速度     
B = 30.111e+06;        %信号带宽
fc = -6900;          %多普勒中心频率
Fa = PRF;

% Ka = 1733;

lambda = c/f0;
Kr = -B/Tr;
% Kr = -7.2135e+11;

[Na_tmp, Nr_tmp] = size(data_1);
kai = kaiser(Nr_tmp, 2.5);
Ext_kai = repmat(kai', Na_tmp, 1);
data_1 = data_1.*Ext_kai;
[Na, Nr] = size(data_1);
data = zeros(Na+Na, Nr+Nr);
data(Na/2:Na+Na/2-1, Nr/2:Nr/2+Nr-1) = data_1;
[Na,Nr] = size(data);


R0 = start*c/2;
theta_rc = asin(fc*lambda/(2*Vr));
Ka = 2*Vr^2*cos(theta_rc)^3/(lambda*R0);
R_eta_c = R0/cos(theta_rc);
eta_c = 2*Vr*sin(theta_rc)/lambda;

f_tau = fftshift((-Nr/2:Nr/2-1)*(Fs/Nr));
f_eta = fc + fftshift((-Na/2:Na/2-1)*(Fa/Na));

tau = 2*R_eta_c/c + (-Nr/2:Nr/2-1)*(1/Fs);
eta = eta_c + (-Na/2:Na/2-1)*(1/Fa);

[Ext_time_tau_r, Ext_time_eta_a] = meshgrid(tau, eta);
[Ext_f_tau, Ext_f_eta] = meshgrid(f_tau, f_eta);

R_ref = R_eta_c; % 将参考目标设为场景中心

data = data.*exp(-2j*pi*fc*Ext_time_eta_a);
data_tau_feta = fft(data, Na, 1); % 首先变换到距离多普勒域

成像

CSA 成像中，补余RCMC需要在距离多普勒域实现，一致RCMC需要在二维频域实现。虽然这两个RCMC没有顺序要求，但准备以如图所示的流程进行。
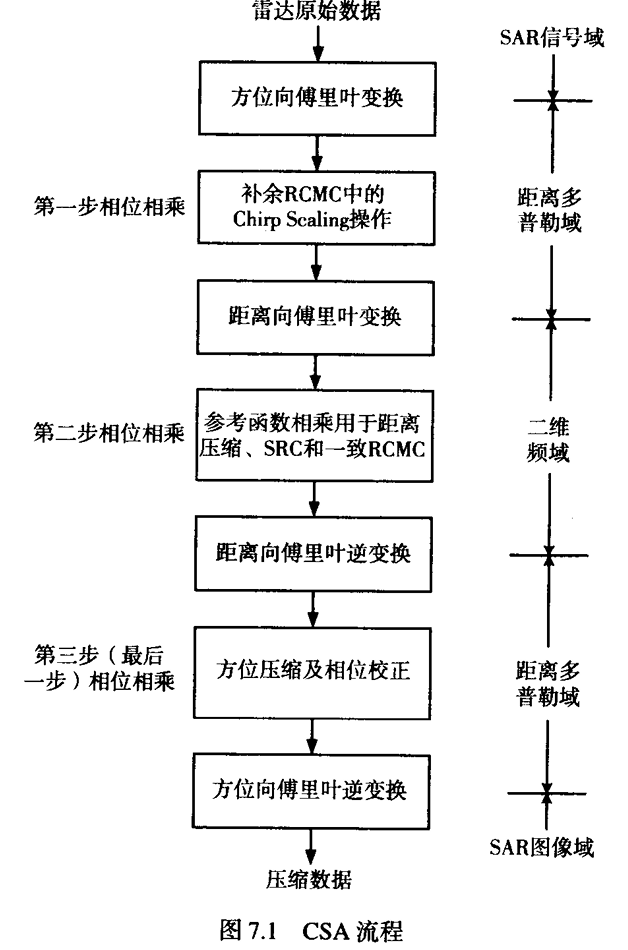
alt text

徙动距离计算

相较于RDA算法，CSA算法的距离压缩与RCMC是一起进行的，没有顺序要求。所以这里首先进行RCMC。为了完成RCMC，需要先计算出RCM。CSA算法要求计算出两种RCM

一致RCM：参考目标的RCM，这里是场景中心的RCM
补余RCM：其他目标的RCM与参考目标的RCM差。
为了计算出RCM，在大斜视角下，我们首先需要计算出徙动因子与随距离变化的距离调频率。

\[D(f_\eta, V_r) = \sqrt{1-\frac{c^2 f_\eta^2}{4V_r^2 f_0^2}}\]

D = sqrt(1-c^2*Ext_f_eta.^2/(4*Vr^2*f0^2));%徙动因子
D_ref = sqrt(1-c^2*fc.^2/(4*Vr^2*f0^2)); % 参考目标的徙动因子（方位向频率中心）

%大斜视角下，距离调频率随距离变化
K_factor = c*R0*Ext_f_eta.^2./(2*Vr^2*f0^3.*D.^3);
Km = Kr./(1-Kr*K_factor); 

由此可以计算出各个RCM

rcm_total = R0./D - R0/D_ref; % 整体rcm
rcm_bulk = R_ref./D - R_ref/D_ref; % 一致rcm（参考点的rcm）
rcm_diff = rcm_total - rcm_bulk; % 补余rcm（整体rcm与参考rcm的差）

RCMC与距离压缩

首先进行补余RCMC，这个操作相当于将回波信号平移RCM个距离单元。

delta_tau = 2*rcm_diff/c; % 补余rcmc的变标移动的时间
Ext_echo_tau = Ext_time_tau_r-2*R_ref./(c*D); %以参考目标为中心

s_sc = exp(2j*pi*Km.*Ext_echo_tau.*delta_tau);
data_tau_feta = data_tau_feta.*s_sc; %变标，完成补余rcmc

然后在二维频域完成距离压缩与一致RCMC

data_ftau_feta = fft(data_tau_feta, Nr, 2);
data_ftau_feta = data_ftau_feta.*exp(2j*pi*(2*rcm_bulk/c).*Ext_f_tau); % 一致rcmc

Hr = exp(1j*pi*(D./(Km.*D_ref)).*Ext_f_tau.^2); 
data_ftau_feta = data_ftau_feta.*Hr; % 距离压缩

方位压缩

最后是方位压缩，需要对附加相位进行补偿

data_tau_feta = ifft(data_ftau_feta, Nr, 2);
R0_RCMC = c*Ext_time_tau_r/2;
Ha = exp(4j*pi*D.*R0_RCMC*f0/c); 
data_tau_feta = data_tau_feta.*Ha; % 方位压缩
offset = exp(-4j*pi*Km.*(1-D./D_ref).*(R0./D-R_ref./D).^2/c^2);
data_tau_feta = data_tau_feta.*offset; %附加相位校正;

data_final = ifft(data_tau_feta, Na, 1);

效果

CSA算法主要在于理解变标。