滑动聚束模式仿真
参数
| 参数名 | 符号 | 值 |
|---|---|---|
| 载频 | $f$ | 5.4 GHz |
| 方位向天线长度 | $L_a$ | 6 m |
| PRF | PRF | 2318 Hz |
| 脉冲宽度 | $T_r$ | 4 $\mu s$ |
| 脉冲带宽 | $B_r$ | 150 MHz |
| 等效雷达速度 | $v_r$ | 7200 m/s |
| 景中心斜距 | $R_c$ | 600 km |
| 波束旋转速度 | $\omega$ | 0.2656 $^\circ/s$ |
| 初始斜视角 | $\theta_c$ | 3 $^\circ$ |
| 合成孔径时间 | $T_a$ | 6 s |
回波生成
仿真实验通过对比条带模式与滑动聚束模式,来观察滑动聚束的聚焦效果。由于仿真使用的成像算法需要大量的插值,仿真使用python 实现,使用GPU 加速仿真。代码省去条带模式
## generate echo
for i in range(self.point_n):
# slide spot
R0_tar = self.point_r[i]
R_eta_spot = cp.sqrt(R0_tar**2 + (self.vr*mat_eta_spot - self.point_y[i])**2)
Wr_spot = (cp.abs(mat_tau_spot - 2 * R_eta_spot / self.c) <= self.Tr / 2)
##滑动聚束工作模式的斜视角一般定义为当天线波束中心指向场景中心点时的斜视角,因此此时景中心旋转角度为0
Wa_spot = cp.sinc(self.La * (cp.arccos(R0_tar / R_eta_spot) - (self.theta_c - self.omega * (mat_eta_spot-self.eta_c_spot))) / self.lambda_)**2
# Tspot_tar = 0.886*self.lambda_*R0_tar/(self.A*self.La*self.vr*cp.cos(self.theta_c)**2)
# Wa_spot = cp.abs(mat_eta_spot-(self.point_y[i]/(self.vr*self.A) + self.eta_c_spot)) < Tspot_tar/2
Phase_spot = cp.exp(-4j * cp.pi * self.f * R_eta_spot / self.c) * cp.exp(1j * cp.pi * self.Kr * (mat_tau_spot - 2 * R_eta_spot / self.c)**2)
S_echo_spot += Wr_spot * Wa_spot * Phase_spot
滑动聚焦模式改变了波束照射方式,通过波束旋转(?)延长目标的照射时间,从而增大多普勒带宽,提高方位向分辨率,其提高因子 $A$ 与虚拟旋转中心的最短斜距 $R_{rot}$ 为
R_rot = vr*cp.cos(theta_c)**2/omega
A = 1 - omega * R0 / (vr * cp.cos(theta_c)**2)
而条带模式的点目标合成孔径时间 $T_f$ 比 $T_a$ 短
Tf = Ta*A
成像
参考论文
W. Xu, Y. Deng, P. Huang and R. Wang, “Full-Aperture SAR Data Focusing in the Spaceborne Squinted Sliding-Spotlight Mode,” in IEEE Transactions on Geoscience and Remote Sensing, vol. 52, no. 8, pp. 4596-4607, Aug. 2014, doi: 10.1109/TGRS.2013.2282863
dramping
def deramping(self, S_echo_spot):
tau_spot = 2*self.Rc/self.c + cp.arange(-self.Nr/2, self.Nr/2) / self.Fr
# old sample interval
self.delta_t1 = 1/self.PRF
self.delta_t2 = 1/(self.B_tot)
# new sample interval
R_tranfer = self.R_rot/cp.cos(self.theta_c)**3
# new sample count
self.P0 = self.lambda_*R_tranfer/(2*self.vr**2*self.delta_t1 *self.delta_t2)
self.P0 = int(cp.round(self.P0))
self.delta_t2 = self.lambda_*R_tranfer/(2*self.vr**2*self.delta_t1 *self.P0)
eta_1 = cp.arange(-self.Na_spot/2, self.Na_spot/2)*(self.delta_t1 )
mat_tau1 , mat_eta_1 = cp.meshgrid(tau_spot, eta_1)
H1 = cp.exp(-1j * cp.pi * self.k_rot * mat_eta_1**2 - 2j*cp.pi*self.feta_c*mat_eta_1)
print("Na_spot, P0:", self.Na_spot, self.P0)
# convolve with H1, similar to the specan algorithm.
# remove the doppler centoid varying
echo = S_echo_spot*H1
temp = cp.zeros((self.P0, self.Nr), dtype=cp.complex128)
temp[self.P0/2-self.Na_spot/2:self.P0/2+self.Na_spot/2, :] = echo # center
# temp[0:self.Na_spot, :] = echo #left
# temp[self.P0-self.Na_spot:self.P0, :] = echo #right
echo = temp
## upsample to P0
echo_ftau_eta = cp.fft.fftshift(cp.fft.fft2((echo), (self.P0, self.Nr)))
## the output azimuth extension
self.T1 = 0.886*self.lambda_/(self.La*self.omega)
print("azimuth time after deramping: ", self.T1, self.P0*self.delta_t2)
# normal ramping, cannot deal with the backfold caused by squint
eta_2 = cp.arange(-self.P0/2, self.P0/2)*(self.delta_t2)
_ , mat_eta_2 = cp.meshgrid(tau_spot, eta_2)
H2 = cp.exp(-1j*cp.pi*self.k_rot*mat_eta_2**2)
echo_ftau_eta_normal = echo_ftau_eta*H2
echo_ftau_feta_normal = (cp.fft.fft(echo_ftau_eta_normal, axis=0))
return echo_ftau_eta, echo_ftau_feta_normal
mosaic and ramping
拼接,从而解决斜视引起的多普勒带宽扩展的backfold
def azimuth_mosaic(self, echo_ftau_eta):
tau_spot = 2*self.Rc/self.c + cp.arange(-self.Nr/2, self.Nr/2) / self.Fr
copy_cnt = int(2*cp.ceil((self.Bf+self.Bsq)/(2*self.PRF)) + 1)
P0_up = self.P0*copy_cnt
print("copy count:", copy_cnt)
echo_mosaic = cp.zeros((P0_up, self.Nr), dtype=cp.complex128)
for i in range(copy_cnt):
echo_mosaic[i*self.P0:(i+1)*self.P0, :] = echo_ftau_eta
## filter, remove the interferential spectrum
feta_up = self.feta_c+(cp.arange(-P0_up/2, P0_up/2) * self.PRF/self.P0)
f_tau = ((cp.arange(-self.Nr/2, self.Nr/2) * self.Fr / self.Nr))
mat_ftau_up, mat_feta_up = cp.meshgrid(f_tau, feta_up)
Hf = cp.abs(mat_feta_up - self.feta_c - 2*self.A*self.vr*(mat_ftau_up)*cp.sin(self.theta_c)/self.c)<self.PRF/2
# Hf = cp.roll(Hf, -(self.Na_spot/2), axis=0)
echo_mosaic_filted = echo_mosaic * Hf
# echo_mosaic_filted = cp.roll(echo_mosaic_filted, (self.Na_spot/2), axis=0)
self.P1 = int(cp.ceil(self.P0*(self.Bf+self.Bsq)/self.Bf))
# self.P1 = self.P0
# delta_t3 = lambda_*R_tranfer/(2*vr**2*self.delta_t1 *P0)
echo_ftau_eta = echo_mosaic_filted[P0_up/2-self.P1/2:P0_up/2+self.P1/2, :]
print("P1", self.P1)
print("new sample rate", 1/self.delta_t2)
# convolve with H2, upsampled signal.
eta_2 = cp.arange(-self.P1/2, self.P1/2)*(self.delta_t2)
_ , mat_eta_2 = cp.meshgrid(tau_spot, eta_2)
H2 = cp.exp(-1j*cp.pi*self.k_rot*mat_eta_2**2)
echo_ftau_eta = echo_ftau_eta*H2
echo_ftau_feta = (cp.fft.fft(echo_ftau_eta, axis=0))
self.T1 = self.delta_t2*self.P1
print("azimuth time after mosaic: ", self.T1)
return echo_mosaic, echo_ftau_eta, echo_ftau_feta
foucs
def wk_focusing(self, echo_ftau_feta, k_rot, eta_c, prf, R_ref):
## RFM
[Na,Nr] = cp.shape(echo_ftau_feta)
f_tau = ((cp.arange(-Nr/2, Nr/2) * self.Fr / Nr))
f_eta = self.feta_c+((cp.arange(-Na/2, Na/2) * prf / Na))
eta = eta_c + cp.arange(-Na/2, Na/2) / prf
tau = 2 * cp.sqrt(self.R0**2 + self.vr**2 * eta_c**2) / self.c + cp.arange(-Nr/2, Nr/2) /self.Fr
mat_tau, mat_eta = cp.meshgrid(tau, eta)
mat_ftau, mat_feta = cp.meshgrid(f_tau, f_eta)
H3 = cp.exp((4j*cp.pi*R_ref/self.c)*cp.sqrt((self.f+mat_ftau)**2 - self.c**2 * mat_feta**2 / (4*self.vr**2)) + 1j*cp.pi*mat_ftau**2/self.Kr)
if k_rot != 0:
H3 =H3*cp.exp(-1j*cp.pi*mat_feta**2/k_rot)
echo_ftau_feta = echo_ftau_feta * H3
## modified stolt mapping
map_f_tau = cp.sqrt((self.f+mat_ftau)**2-self.c**2*mat_feta**2/(4*self.vr**2))-cp.sqrt(self.f**2-self.c**2*mat_feta**2/(4*self.vr**2))
# map_f_tau = cp.sqrt((f+mat_ftau)**2-c**2*mat_feta**2/(4*vr**2))-f
delta = (map_f_tau - mat_ftau)/(self.Fr/Nr) #频率转index
delta_int = cp.floor(delta).astype(cp.int32)
delta_remain = delta-delta_int
## sinc interpolation kernel length, used by stolt mapping
sinc_N = 8
echo_ftau_feta_stolt = self.stolt_interpolation(echo_ftau_feta, delta_int, delta_remain, Na, Nr, sinc_N)
## focusing
## modified stolt mapping, residual azimuth compress
# mat_R = mat_tau * self.c / 2
# echo_tau_feta_stolt = cp.zeros((Na, Nr), dtype=cp.complex128)
# eta_r_c = mat_R * cp.tan(self.theta_c) / self.vr
# if k_rot != 0:
# H4 = cp.exp(4j*cp.pi*(mat_R-R_ref)/self.c * (cp.sqrt(self.f**2-self.c**2*mat_feta**2/(4*self.vr**2)))) * cp.exp(2j*cp.pi*mat_feta*eta_r_c - 2j*cp.pi*mat_feta*self.feta_c/k_rot)
# echo_tau_feta_stolt = cp.fft.ifft((echo_ftau_feta_stolt), axis = 1)
# echo_tau_feta_stolt = echo_tau_feta_stolt * H4
# else:
# H4 = cp.exp(4j*cp.pi*(mat_R-R_ref)/self.c * (cp.sqrt(self.f**2-self.c**2*mat_feta**2/(4*self.vr**2)))) * cp.exp(2j*cp.pi*mat_feta*eta_r_c)
# echo_tau_feta_stolt = cp.fft.ifft((echo_ftau_feta_stolt), axis = 1)
# echo_tau_feta_stolt = echo_tau_feta_stolt * H4
# echo_ftau_feta_stolt = cp.fft.fft(echo_tau_feta_stolt, axis = 1)
echo_stolt = (cp.fft.ifft2((echo_ftau_feta_stolt)))
echo_no_stolt = (cp.fft.ifft2((echo_ftau_feta)))
return echo_stolt, echo_no_stolt
resolve backfold
def postfilter(self, echo_spot):
delta_f1 = 1/(self.T1) ## should be equal to 1/(self.delta_t2*self.P1)
f_eta1 = self.feta_c+(cp.arange(-self.P1/2, self.P1/2) * delta_f1)
f_tau = ((cp.arange(-self.Nr/2, self.Nr/2) * self.Fr / self.Nr))
_, mat_feta1 = cp.meshgrid(f_tau, f_eta1)
echo_tau_feta = cp.fft.fft(echo_spot, axis=0)
kx = -(self.A-1)*self.ka/self.A
## azimuth frequency interval
## extend the azimuth time
delta_f2 = cp.array(2/(self.Tx0+self.Tx1))
self.P2 = int(cp.ceil(cp.abs((kx/(delta_f1*delta_f2)))))
delta_f2 = cp.abs(kx/(self.P2*delta_f1))
print("P2: ", self.P2)
f_eta2 = self.feta_c+(cp.arange(-self.P2/2, self.P2/2) * delta_f2)
_, mat_feta2 = cp.meshgrid(f_tau, f_eta2)
# convolve with H5
## deramping
H5 = cp.exp(1j*cp.pi*mat_feta1**2/kx)
echo_tau_feta = echo_tau_feta * H5
## change sample count
echo_tau_feta = echo_tau_feta[self.P1/2-self.P2/2:self.P1/2+self.P2/2, :]
echo_tau_feta_deraming = cp.fft.ifft(echo_tau_feta, axis=0)
#ramping back
H6 = cp.exp(1j*cp.pi*mat_feta2**2/kx)
echo_tau_feta = echo_tau_feta_deraming * H6
echo_spot_post = cp.fft.ifft(echo_tau_feta, axis=0)
print("azimuth time after postfilter: ", 1/delta_f2)
self.delta_t3 = (1/delta_f2) / self.P1
eta = cp.arange(-self.P2/2, self.P2/2) * self.delta_t3
tau = 2 * self.Rc / self.c + cp.arange(-self.Nr/2, self.Nr/2) /self.Fr
_, mat_eta = cp.meshgrid(tau, eta)
H7 = cp.exp(-1j*cp.pi*kx*mat_eta**2)
echo_spot_post = echo_spot_post * H7
return echo_spot_post, echo_tau_feta_deraming
效果
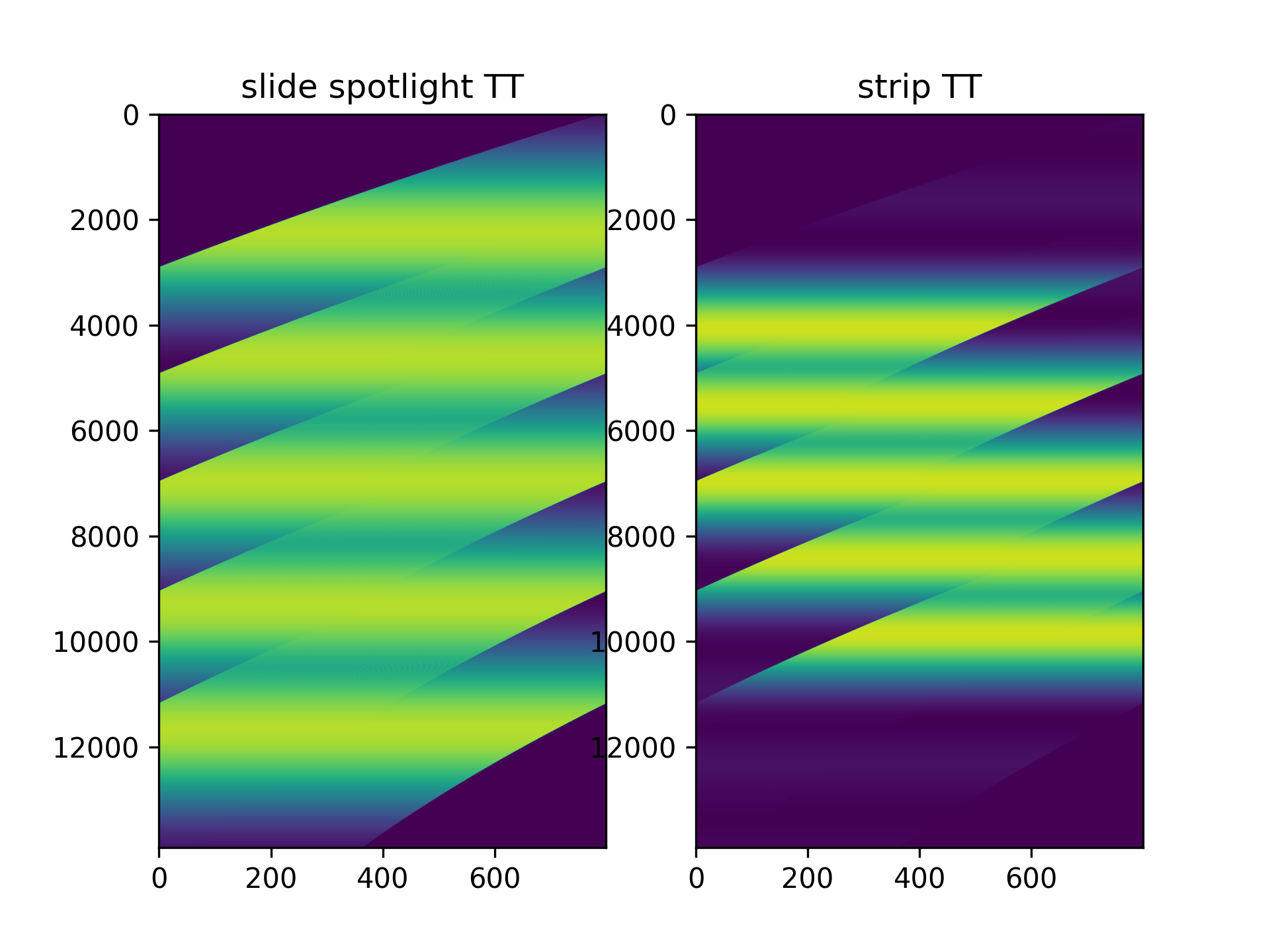
其中左边为slide spot回波, 右边为条带模式回波。可以很明显的看出,滑动聚束模式点目标的回波在方位向的时间宽度是大于条带模式的,但相应的成像区域的大小缩减。
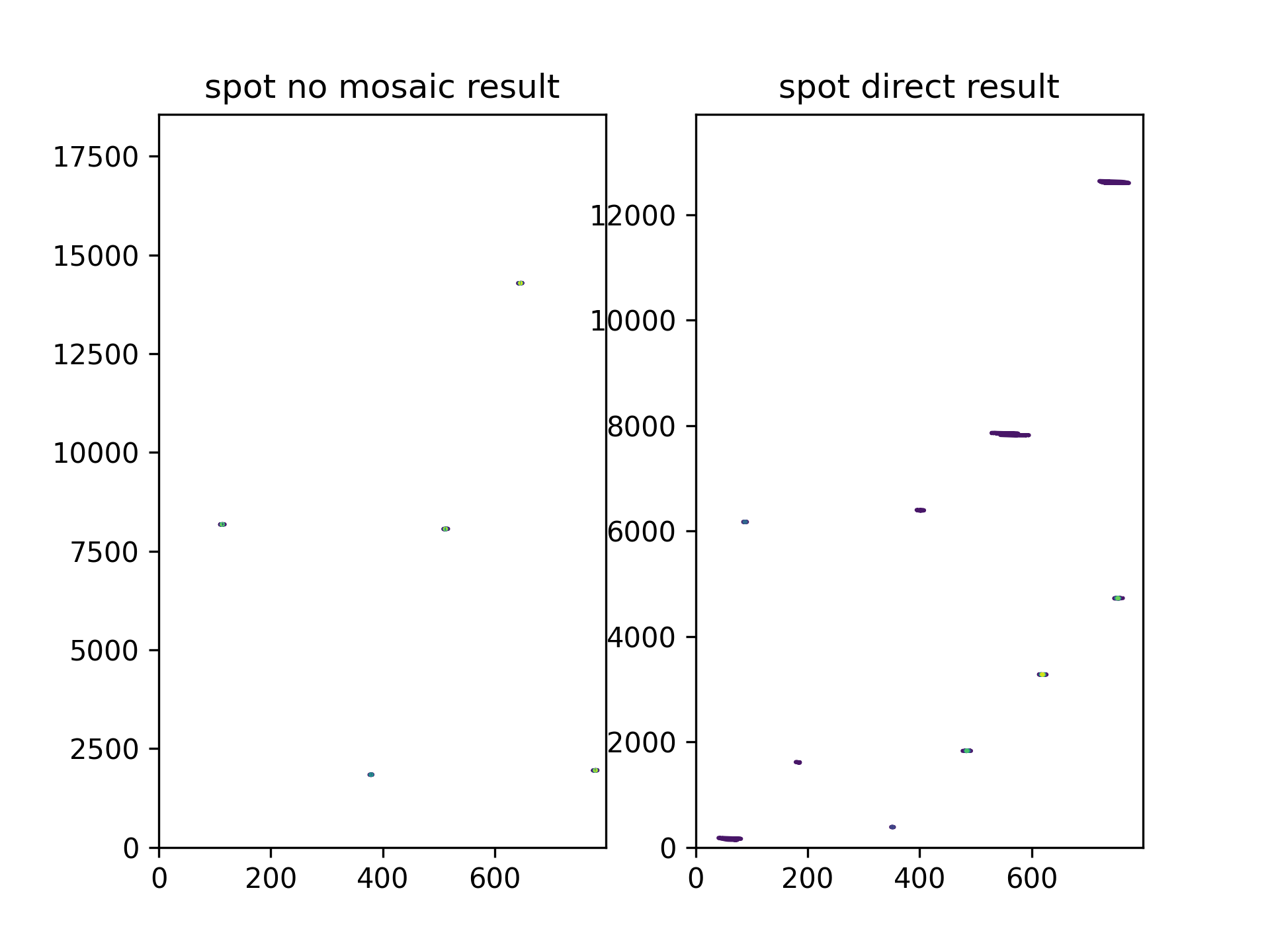
左边为使用经典two steps focus 预处理的效果,可以发现依然存在backfold。右边为没有任何预处理直接成像的效果。
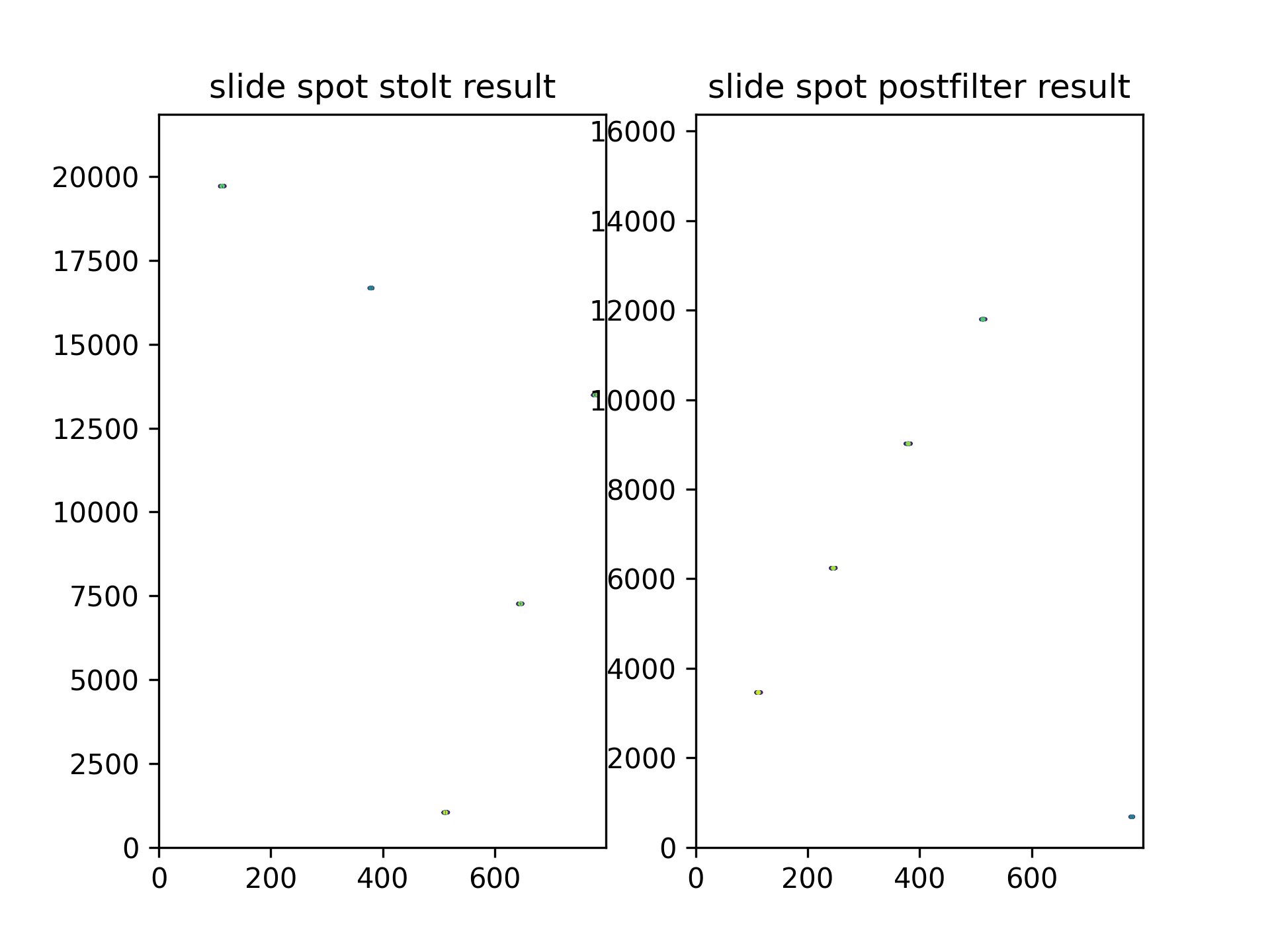
左图为通过拼接去除斜视影响的效果。右边为完整处理的效果。