简单sar系统设计仿真

参数与初始化

EarthMass = 6e24;
Gravitational = 6.67e-11;
B = 125.18e6;
T = 40e-6;
f = 9.65e9;
H = 576e3;
c = 299792458;
R_en = 6371e3;
Rs = H+R_en;
Rt = R_en;
v = sqrt(Gravitational*EarthMass/Rs); %飞行速度
lamdba = c/f; 
delta_az = 2; % 方位向分辨率
delta_ar = 2; % 距离向分辨率

斑马图计算

%% 斑马图
prf = 1000:2000;
tau_rp = 5e-6;
% gamma = acos((R^2+Rs^2-Rt^2)/2*R*Rs);

frac_min = -(tau_rp+T)*prf; % 发射约束
frac_max = (tau_rp)*prf;

int_min = min(floor(2*H*prf/c));
int_max = max(ceil(2*sqrt(Rs^2-Rt^2)*prf/c));

figure("name", "斑马图");

% 遍历尽可能多的干扰，这里应该有上下限的，但考虑到只显示部分，便没有计算。
for i = 0:int_max  

    R1 = (i+frac_min)*c./(2*prf);
    gamma_cos = (R1.^2+Rs^2-Rt^2)./(2*R1*Rs);
    tmp_gamma_cos = (abs(gamma_cos)<=1).*gamma_cos;
    gamma_cos = (1-(abs(gamma_cos)<=1))+tmp_gamma_cos;
    gamma = acos(abs(gamma_cos));
    belta = asin(R1.*sin(gamma)/R_en);
    W1 = R_en*belta/1000;
    gamma1 = rad2deg(gamma);

    plot(prf,gamma1);
    hold on;

    Rn = (i+frac_max)*c./(2*prf);
    gamma_cos = (Rn.^2+Rs^2-Rt^2)./(2*Rn*Rs);
    tmp_gamma_cos = (abs(gamma_cos)<=1).*gamma_cos;
    gamma_cos = (1-(abs(gamma_cos)<=1))+tmp_gamma_cos;
    gamma = acos(abs(gamma_cos));
    belta = asin(R1.*sin(gamma)/R_en);
    W2 = R_en*belta/1000;
    gamma2 = rad2deg(gamma);
    plot(prf,gamma2);
    hold on;
    pic = fill([prf, fliplr(prf)], [gamma1, fliplr(gamma2)], 'b');
    set(pic, 'facealpha', 0.1);
end


% 星下点干扰
for i  = 0:5
    R = (2*H/c+i./prf)*c/2;
    gamma_cos = (R.^2+Rs^2-Rt^2)./(2*R*Rs);
    tmp_gamma_cos = (abs(gamma_cos)<=1).*gamma_cos;
    gamma_cos = (1-(abs(gamma_cos)<=1))+tmp_gamma_cos;
    gamma = acos(abs(gamma_cos));
    belta = asin(R.*sin(gamma)/R_en);
    W1 = R_en*belta/1000;
    gamma1 = rad2deg(gamma);
    plot(prf,gamma1);
    hold on;

    R = (2*H/c+i./prf+T*2)*c/2;
    gamma_cos = (R.^2+Rs^2-Rt^2)./(2*R*Rs);
    tmp_gamma_cos = (abs(gamma_cos)<=1).*gamma_cos;
    gamma_cos = (1-(abs(gamma_cos)<=1))+tmp_gamma_cos;
    gamma = acos(abs(gamma_cos));
    belta = asin(R.*sin(gamma)/R_en);
    W2 = R_en*belta/1000;
    gamma2 = rad2deg(gamma);
    plot(prf,gamma2);
    hold on;
    pic = fill([prf, fliplr(prf)], [gamma1, fliplr(gamma2)], 'r');
    set(pic, 'facealpha', 0.1);
end

xlabel("PRF/Hz");
ylabel("下视角");
ylim([18, 50]);

这里干扰公式参照

合成孔径雷达系统与信号处理 [（美）柯兰德著] 2014年版

朱力,于立.星载合成孔径雷达(SAR)斑马图仿真与研究.计算机仿真,2003,20(5):123-126

我仿真的时候，书中的公式效果不是很好。最终效果如图斑马图
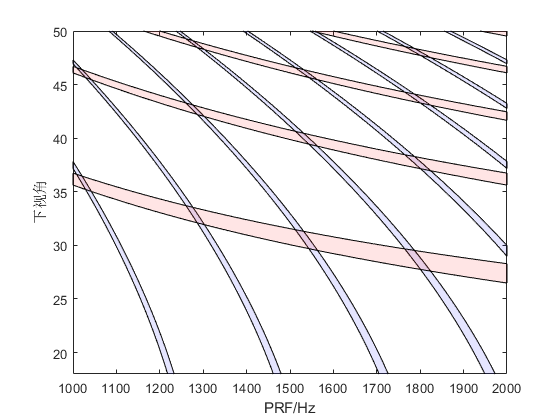
其中有颜色的是干扰区，蓝色的是发射干扰，红色的是星下点回波干扰。

AASR

这里用于对照的论文里，雷达系统是单孔径发射，多孔径接收的。需要计算接收端的重构滤波器，关于重构滤波器的理论是比较简单的，这里就不赘述。

%% AASR

% 方位向天线参数
drz = 3.3;
dtz = 4.4;

% vg = (R_en*v/Rs)*cos(belta);
prf = 1000:2000;
theta_min = deg2rad(31.95); % 视角范围
theta_max = deg2rad(38.8);
theta = (theta_min+theta_max)/2;

Bd = 3418; % 多普勒带宽
fa_band = -Bd/2:Bd/2;
m = 3;

G_tx = sinc(fa_band*dtz/(2*v)).^2; % 计算方向图
G_rx = sinc(fa_band*drz/(2*v)).^2;
G = G_tx.*G_rx;
len = length(prf);

len_band = length(fa_band);
P_re = zeros(3,3,len_band,len);
aasr_deno = trapz(fa_band, G); % 积分得到aasr 分母

% 计算重构滤波器
for j = 1:len
    G_tmp = G;
    for i = 1:len_band
        H_re = zeros(3,3);
        for k = 1:3
            for n = 1:3
                H_re(k,n) = exp(-1j*pi*(n*drz/v)*(fa_band(i)+k*prf(j)));
            end
        end
        P_re(:,:,i,j) = inv(H_re);
    end
end


aasr_num = zeros(1,len); % aasr 分子
aasr = zeros(1,len);
for j = 1:len
    for i = 1:m
        if(i == 0)
            continue;
        end
        G_tmp_tx = sinc((fa_band+i*prf(j))*dtz/(2*v)).^2;
        G_tmp_rx = sinc((fa_band+i*prf(j))*drz/(2*v)).^2;
        G_tmp = G_tmp_rx.*G_tmp_tx;

        % 计算每个频率的混叠
        H_re = zeros(3,3);
        for h = 1:len_band
            H_re = zeros(3,3);
            for k = 1:3
                for n = 1:3
                H_re(k,n) = exp(-1j*pi*(n*drz/v)*((fa_band(h)+i*prf(j)+k*prf(j))));
                end
            end
            tmp = G_tmp(h)*H_re*P_re(:,:,h,j);
            G_tmp(h) = tmp(1,1);
        end
        aasr_num(j) = abs(2*trapz(fa_band, G_tmp))+aasr_num(j);
    end
    aasr(j) = aasr_num(j)/aasr_deno;
    aasr(j) = 10*log10(aasr(j));
end

figure("name", "AASR");
plot(prf, aasr);
xlabel("PRF [Hz]")
ylabel("AASR [dB]")

最终效果始终与论文有比较小的偏差，不知道是什么原因 aasr
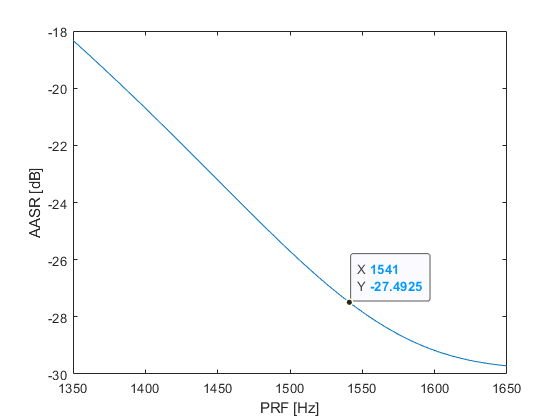
可以看到当PRF等于1541 Hz的时候，AASR为-27.4925dB，是比较好的。

RASR

距离向接收端也是多孔径的，但是不用考虑混叠。

%% RASR
n = 10;

Wn =  (366:0.1:478)*1e3; % 地距范围
belta = Wn/R_en;

vg = Rt*cos(belta)*v/Rs; % 波束移动速度
vg = (max(vg)+min(vg))/2;

Bd = 0.886*vg/delta_az; %这里计算出多普勒带宽，应该放在前面


len = length(Wn);
fp = 1541; % PRF
gamma0 = deg2rad(35.375); % 中心视角，这里也当作天线法线的角

eta_c = asin(Rs*sin(gamma0)/Rt);
Be = 1.1*c/(2*2*sin(eta_c)); % 距离向带宽，系数1.1是提供裕度
Rn = sqrt(Rs^2+Rt^2-2*Rs*Rt*cos(belta));

gamma_cos = (Rn.^2+Rs^2-Rt^2)./(2*Rn*Rs); % 计算下视角
tmp_gamma_cos = (abs(gamma_cos)<=1).*gamma_cos;
gamma_cos = (1-(abs(gamma_cos)<=1))+tmp_gamma_cos;
gamma = acos(abs(gamma_cos));

eta_sin = Rs*sin(gamma)/Rt;
eta = asin(eta_sin);

hr = 0.886*lambda*2*max(Rn)*tan(max(eta))/(c*T); % 接收孔径大小
N = 32; % 接收子孔径数目
dre = hr / N; % 接收子孔径大小

phi0 = gamma-(gamma0);

dte = 0.886*lambda/(max(gamma)-min(gamma)); % 发射孔径大小

Gr = sinc(dre*sin(phi0)/lambda).^2; %天线增益，去掉系数
Gt = sinc(dte*sin(phi0)/lambda).^2; 



Si = N^2*Gr.*Gt./(Rn.^3.*eta_sin);
Sai = zeros(1,len);

R_max = sqrt(Rs^2-Rt^2);

for i = -n:n
    if(i == 0) 
        continue;
    end

    Rij = Rn+i*(1/fp)*c/2;
    range = (Rij>=H&Rij<=R_max); % 确认斜距范围
    Rij = range.*Rij + (1-range)*min(Rn);
    gamma_cos = (Rij.^2+Rs^2-Rt^2)./(2*Rij*Rs);
    gammaij = acos(abs(gamma_cos));
    phi = gammaij-(gamma0);
    Grij = sinc(dre*sin(phi)/lambda).^2;
    Gtij = sinc(dte*sin(phi)/lambda).^2;
    eta_sinij = Rs*sin(gammaij)/Rt; 
    A = 0;
    for k = 1:N
        A = A+exp(1j*2*pi*(k-1)*dre*(sin(phi)-sin(phi0))/lambda);
    end
    A = abs(A);
    Sai = range.*(Grij.*Gtij.*A.^2./(Rij.^3.*eta_sinij))+Sai;

end

rasr = 10*log10(Sai./Si);
figure("name", "RASR");
plot(Wn/1e3, rasr);


xlabel("Ground Range [km]")
ylabel("RASR [dB]")

这里地距范围由斑马图确定的。先由斑马图确定下视角，再由下视角确定地距。 rasr
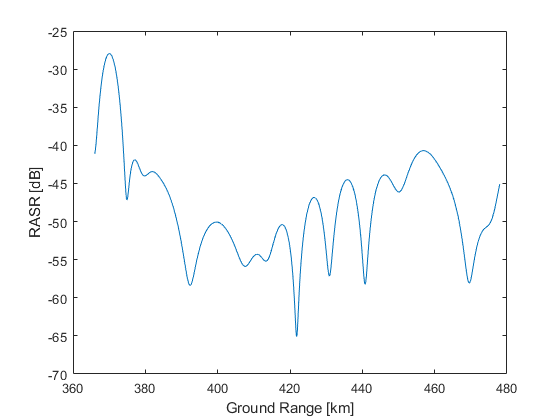
最终效果与论文偏差较大，而且计算得出的天线参数也与论文不同

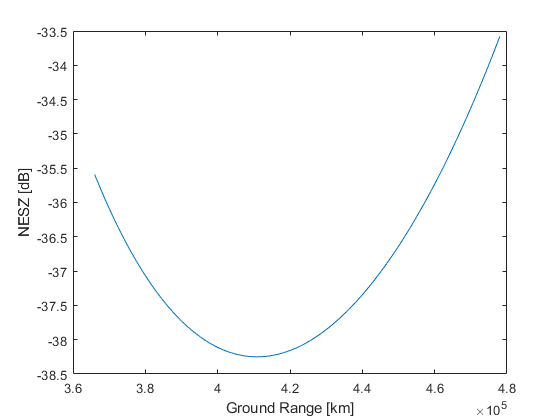
NESZ

NESZ 计算时，参考论文里有很多参数没给，我就设了一些值

figure("name", "NESZ");

T0 = 290; % 等效温度
F = 3; % 噪声系数
L = 1; % 系统损耗

K = 1.38e-23; %玻尔兹曼常数
P = 4000; %发射功率
Na = 3;
Ne = N;

Ar = 0.6*hr*drz;
At = 0.6*dtz*dte;
Gr = (4*pi*Ar/(lambda^2))*Gr; % 添上系数
Gt = (4*pi*At/(lambda^2))*Gt;

Nrg = T*B; % 距离向压缩比
Naz = lambda*Rn*fp/(2*delta_az*v);
SNR_sigma = (Na*Ne*P*Nrg*lambda^2*Naz.*Gr.*Gt)./((4*pi)^3*Rn.^4*K*T0*B*F*L);
sigma = (2*B*eta_sin)/(c*delta_az);

% nesz = sigma./SNR_sigma;
nesz = (4*(4*pi)^3*K*T0*F*L*v*B.*eta_sin.*Rn.^3)./(Ne*Na*P.*Gt.*Gr*lambda^3*c*T*fp);
nesz = 10*log10(nesz);
plot(Wn, nesz);

xlabel("Ground Range [km]")
ylabel("NESZ [dB]")

NESZ计算比较简单，主要在于理解雷达方程。

nesz