方位向多孔径点目标仿真 -- 经典重构算法

仿真参数

参数	符号	值
载波频率	$f_0$	$30 GHz$
光速	$c$	$299792458 m/s$
卫星轨道高度	$H$	$580 km$
卫星速度	$V_s$	$7560 m/s$
方位向接收子孔径长度	$d_{az,rx}$	$1.6 m$
子孔径数目	$N_{az}$	7
斜视角	$\theta_{rc}$	$0$
最近斜距	$R_0$	$740 km$
脉冲时长	$T_r$	$110 \mu s$
脉冲带宽	$B_r$	$26 MHz$
距离向采样率	$F_r$	$1.2B_r$

仿真代码

仿真是在服务器上跑的，远程链接使用不了matlab，使用python 作为替代
仿真软件：python
库：cupy matplotlib.pyplot

回波生成

相较于经典的sar系统，方位向多孔径sar系统的不同之处主要表现于发射路径与接收路径的不同，不同孔径形成不同的接收路径，构成不同的空域采样点，从而合并后能够得到完整的多普勒频率。

point = cp.array([0, 0])
S_echo = cp.zeros((Naz, Na, Nr), dtype=cp.complex128)
for i in range(Naz):
    ant_dx = (i) * daz_rx

    R_point = cp.sqrt((R0 * cp.sin(phi) + point[0])**2 + H**2)
    point_eta_c = (point[1] - R_point * cp.tan(theta_rc)) / Vr
    R_eta_tx = cp.sqrt(R_point**2 + (Vr * mat_eta - point[1])**2)

    mat_eta_rx = mat_eta + ant_dx / Vs
    R_eta_rx = cp.sqrt(R_point**2 + (Vr * mat_eta_rx - point[1])**2)

    Wr = (cp.abs(mat_tau - (R_eta_tx+R_eta_rx) / c) < Tr / 2)
    Wa = (daz_rx * cp.arctan(Vg * (mat_eta - point_eta_c) / (R0 * cp.sin(phi) + point[0]) / lambda_)**2) <= Ta / 2

    echo_phase_azimuth = cp.exp(-1j * 2 * cp.pi * f0 * (R_eta_rx + R_eta_tx) / c)
    echo_phase_range = cp.exp(1j * cp.pi * Kr * (mat_tau - (R_eta_tx + R_eta_tx) / c)**2)
    S_echo[i, :, :] = Wr * Wa * echo_phase_range * echo_phase_azimuth

这个回波生成代码没有考虑天线方向图，即主瓣外的增益视为0，所以无法仿真带外频率的影响。

重构滤波器生成

使用如下的方位向多孔径的系统响应

\[H_j(f) = exp(-j \pi \frac{\Delta x_j}{v_s} f)\]

如果空域采样各不相同，则存在逆，用于恢复原始频谱。注意传入的方位向频率与原始未混叠的多普勒频谱相对应，即从负到正，中心频率为0，按顺序填入系统响应矩阵。

P = cp.zeros((Na, Naz, Naz), dtype=cp.complex128)
H = cp.zeros((Na, Naz, Naz), dtype=cp.complex128)
prf = Fa

# 计算方位向响应
for k in range(Naz):
    for n in range(Naz):
        H_matrix[:, k, n] = cp.exp(- 1j * cp.pi * (n * daz_rx) / Vs * (f_eta + (k-(Naz-1)/2) * prf))
# 计算重构滤波器
for j in range(Na): 
    P_matrix[j] = cp.linalg.inv(H_matrix[j])

成像处理

先进行距离向压缩

S_r_compress = cp.zeros((Naz, Na, Nr), dtype=cp.complex128)
for i in range(Naz):
    echo = cp.squeeze(S_echo[i, :, :])
    Hr = (cp.abs(mat_f_tau) <= Br / 2) * cp.exp(1j * cp.pi * mat_f_tau**2 / Kr)
    S1_ftau_eta = cp.fft.fft(echo, Nr, axis=1)
    S1_ftau_eta = S1_ftau_eta * Hr
  
    S1_tau_eta = cp.fft.ifft(S1_ftau_eta, Nr, axis=1)
    S2_tau_feta = cp.fft.fft(S1_tau_eta, Na, axis=0)
    S_r_compress[i, :, :] = S2_tau_feta

然后对方位向进行升采样

uprate = Naz
f_eta_upsample = fnc + cp.fft.fftshift(cp.arange(-Na * uprate / 2, Na * uprate / 2, 1) * (Fa / Na))
t_eta_upsample = eta_c + cp.arange(-Na * uprate / 2, Na * uprate / 2, 1) * (1 / (Fa * uprate))

mat_tau_upsample, mat_eta_upsample = cp.meshgrid(tau, t_eta_upsample)
mat_f_tau_upsample, mat_f_eta_upsample = cp.meshgrid(f_tau, f_eta_upsample)

构建对比数据，对比数据通过按照采样时间重排各个孔径的信号得到。之后也需要方位压缩

S_ref = cp.zeros((Na*Naz, Nr), dtype=cp.complex128)
for i in range(Na):
    for j in range(Naz):
        S_ref[i*Naz+j,:] = S_echo[Naz-j-1,i,:]

Hr = (cp.abs(mat_f_tau_upsample) <= Br / 2) * cp.exp(1j * cp.pi * mat_f_tau_upsample**2 / Kr)
S_ref_ftau = cp.fft.fft(S_ref, Nr, axis=1)
S_ref_ftau = S_ref_ftau * Hr
S_ref = cp.fft.ifft(S_ref_ftau, Nr, axis=1)
S_ref = cp.fft.fft(S_ref, Na*uprate, axis=0)
S_ref = cp.fft.fftshift(S_ref, axes=0)

重建频谱，注意频率中心对齐。

out_band = cp.zeros((Naz, Na, Nr), dtype=cp.complex128)
out_band_ref = cp.zeros((Naz, Na, Nr), dtype=cp.complex128)
S_out = cp.zeros((Na*uprate, Nr), dtype=cp.complex128)

for i in range(Na):
    aperture = cp.squeeze(S_r_compress[i, :, :])
    P_aperture = cp.squeeze(P_matrix[i, :, :])
    tmp = aperture @ P_aperture
    for j in range(Naz):
        out_band[j, i, :] = tmp[:, j]

for j in range(Naz):
    S_out[j * Na: (j + 1) * Na, :] = cp.fft.fftshift(cp.squeeze(out_band[j, :, :]), axes=0) # 确保连续性

之后就是距离徙动校正，方位压缩与绘图，就不再赘述。

分析

需要注意的是，由于回波生成时没有考虑天线方向图的作用，所以多普勒频谱外的频率所导致的混叠不能反映在仿真中。但对于多普勒频谱内的重建以及混叠抑制，是可以很好的反映的。

uniform PRF

当 $PRF = 2V_s/d_{az,rx} = 1350$ 时，构成最佳的空域采样分布，即经过重构滤波器处理后，方位模糊比在预期的PRF范围较低。通过重排各个孔径的数据，也能得到一致的结果。

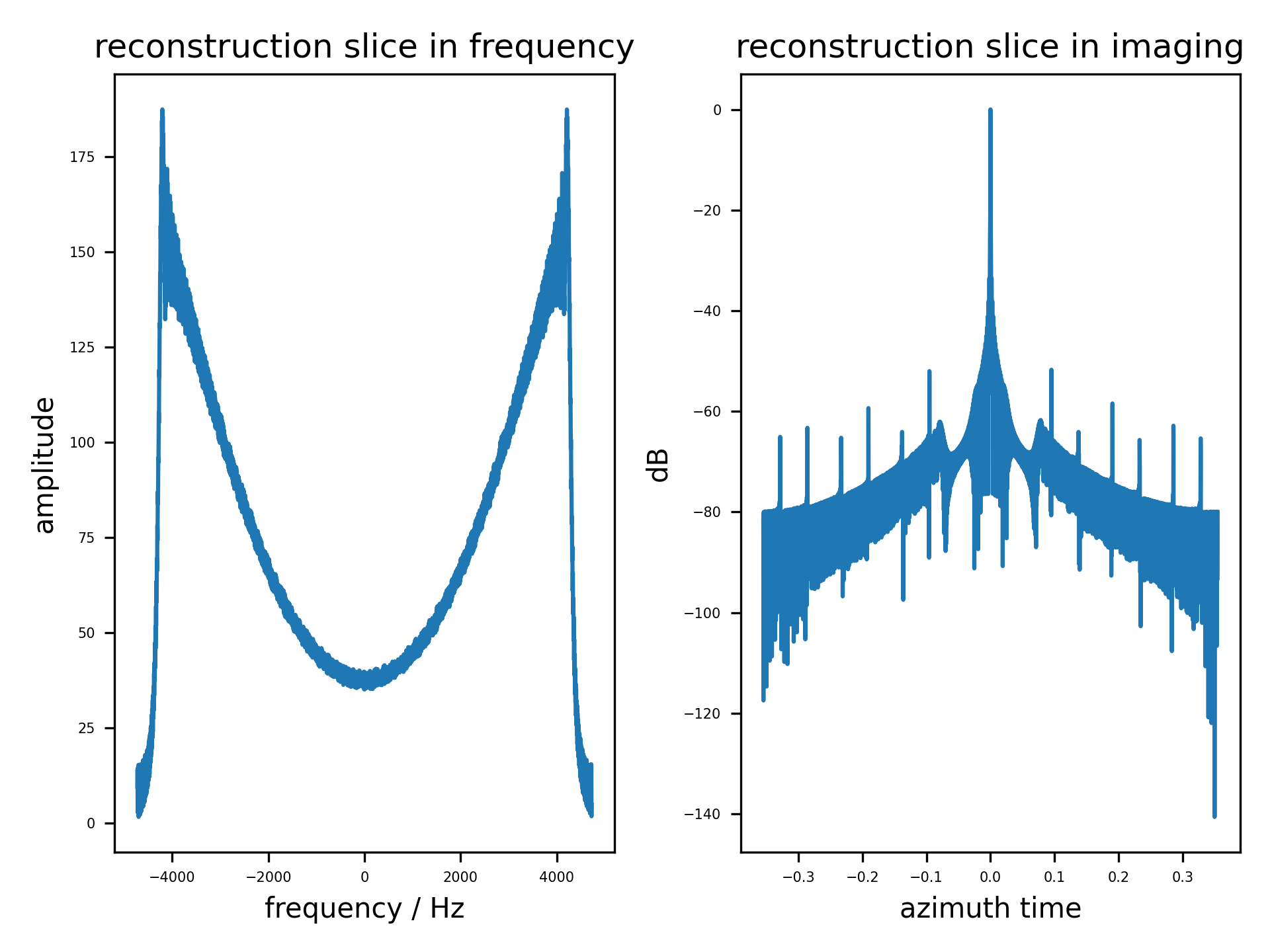
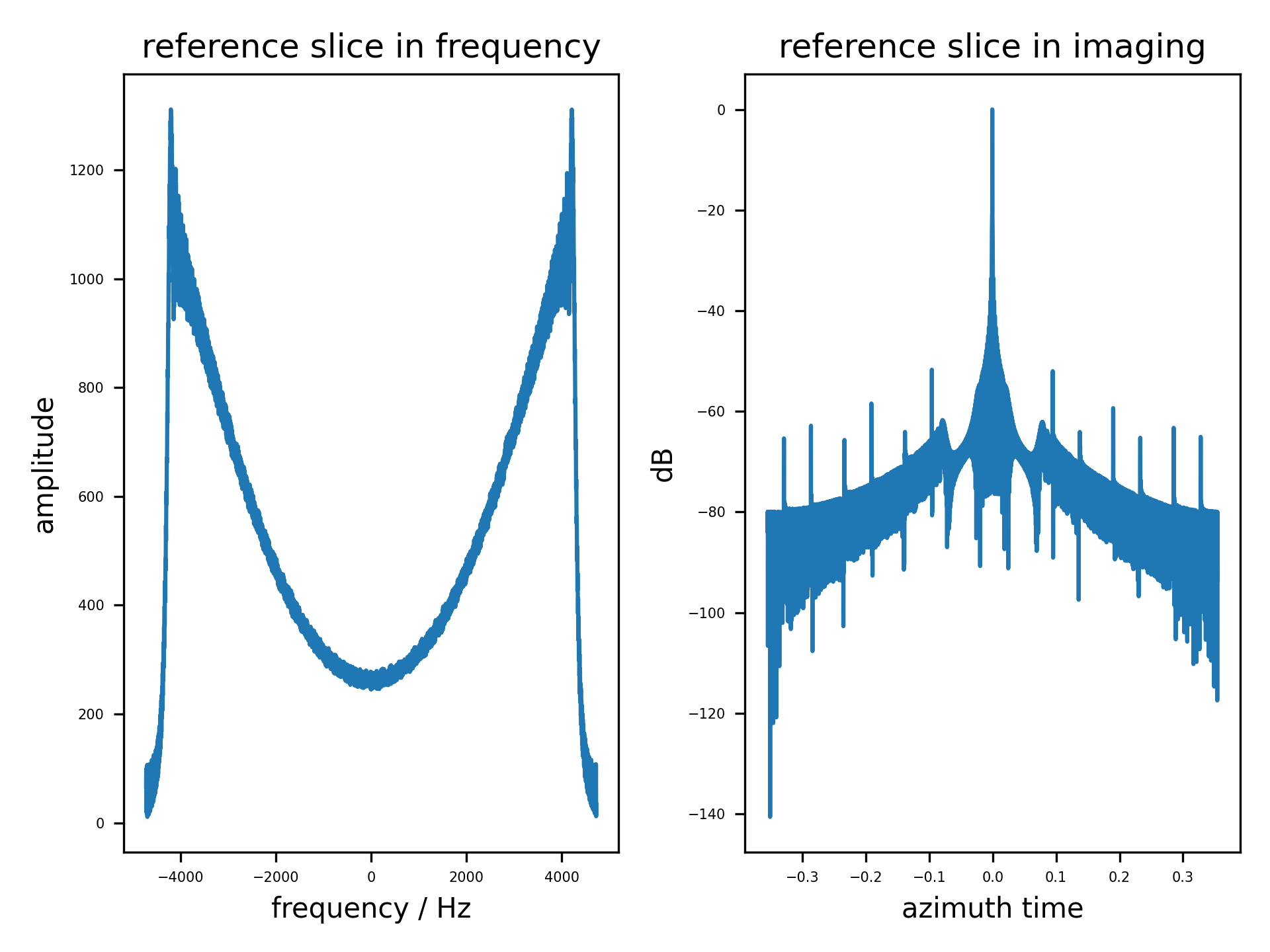
alt text

从图中可以看出，重构滤波器在此PRF上，并没有与简单的重排多孔径数据的效果拉开差距。

not uniform PRF

当 $PRF \neq 2V_s/d_{az,rx}$ 时，比如 $PRF = 2V_s/d_{az,rx} + 100 = 1450$ 时，重排数据便不能得到无混叠的数据，但重构滤波器的输出依然可用，只是方位模糊比下降。

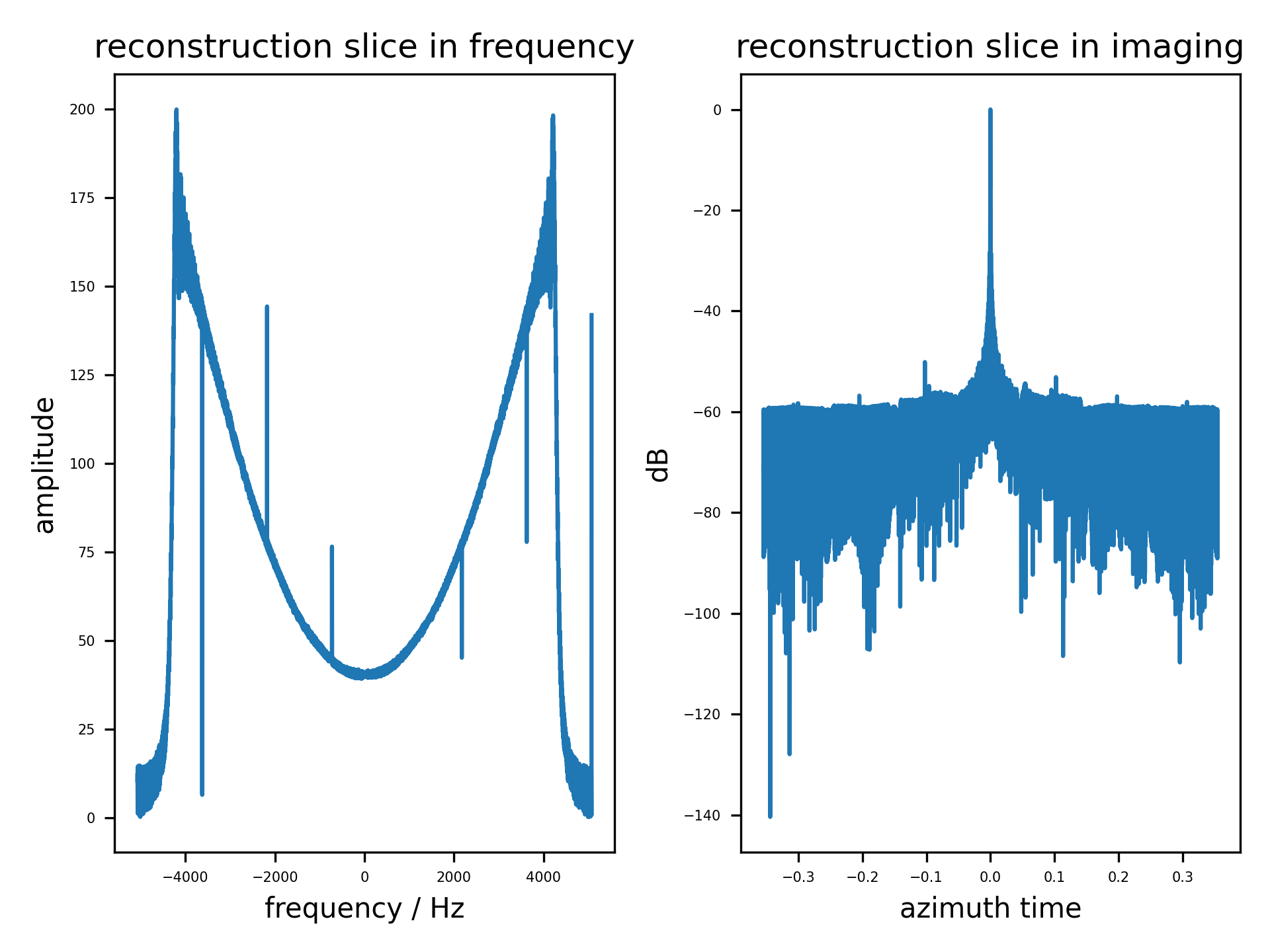
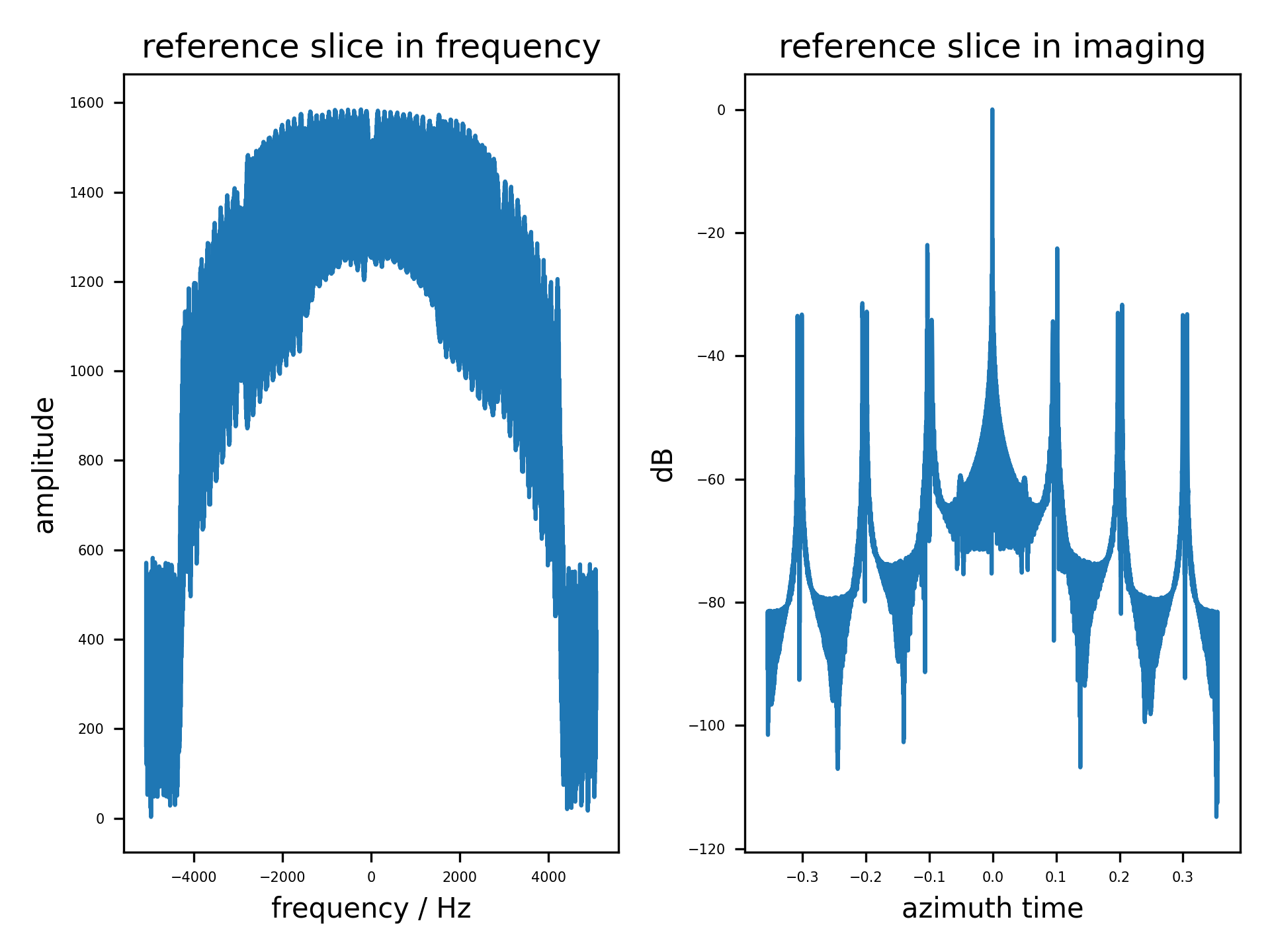
alt text

图中可以看到通过重排数据的方式重建多普勒信号已经难以抑制混叠，方位模糊非常严重。而重构滤波器的输出效果依旧非常好。需要注意到的是，重构滤波器的输出频谱中出现的异常点，这是源于仿真时方位向系统响应矩阵与方位向频率轴未对齐，导致重构矩阵与孔径频谱的方位向频率错配导致的。