模糊分析
距离模糊
成因
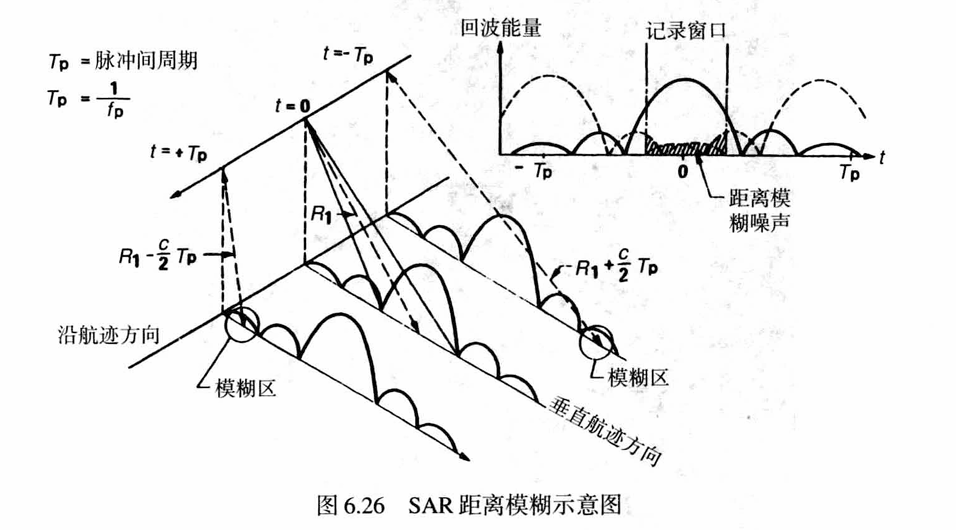
距离模糊是由与所需回波同时到达天线的前一个和后一个脉冲的回波造成的。天线辐射时,除了测绘带散射天线方向图的主瓣外,测绘带以外的地方也会散射天线方向图的旁瓣。由于斜距的不同,旁瓣的散射不会反馈到当前的PRI中,而是出现延时。如果斜距之差刚好满足
\[\Delta R = j\frac{c}{2f_{PRF}},j = \pm1,\pm2,\cdots,\pm n\]则旁瓣的回波会反馈到之前或者之后的回波中。由于距离的问题,一个脉冲从发射到接收需要几个脉冲周期的时间。为了避免邻近脉冲的主瓣的影响,显然PRI需要满足
\[PRI > \frac{2\lambda R tan\eta}{c Wa}\]$Wa$ 为天线宽度,与距离向有关。
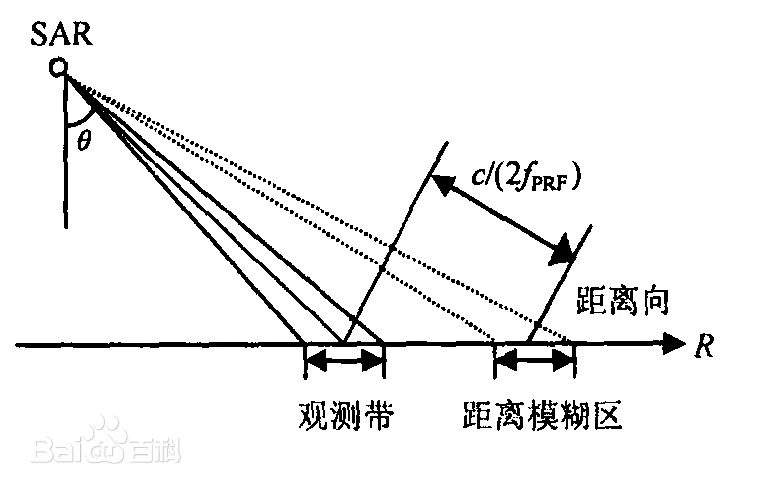
如果所示,不是主瓣干扰,那么应该是同一时间的旁瓣干扰。对应的斜距为
\[R_j = R \pm \Delta R = R \pm j\frac{c}{2 f_{PRF}},j = \pm 1, \pm 2, \cdots, \pm n\]评估方式
距离模糊使用RASR进行描述。此时PRF已经被给定,这里我们设为$f_p$。RASR 被定义为想要的信号功率和距离模糊产生的干扰功率之比。此时噪声可以近似相同,使用雷达方程可以得出
\[RASR = \sum_{j=-n}^n \frac{SNR_j}{SNR}\]$SNR_j$为距离模糊的信号,带入实际的雷达方程,可以化简得到
\[RASR = \sum_{j=-n}^n \frac{\sigma_j^0 G_j^2 / (R_j^3 sin\eta_j)}{\sigma^0 G^2 / R^3 sin \eta}\]G为天线增益,上述表达式中双程为$G^2$。如果收发天线不同,需要改为 $G^tG^r$
方位模糊
成因
方位模糊是由某个PRF上的方位向频谱的有限采样造成的。SAR的多普勒频谱不是严格带限的(由天线旁瓣造成),由于多普勒频谱是由PRF间隔重复的,所以PRF外的频率分量就折回到频谱的主要部分中,对主要部分产生影响。
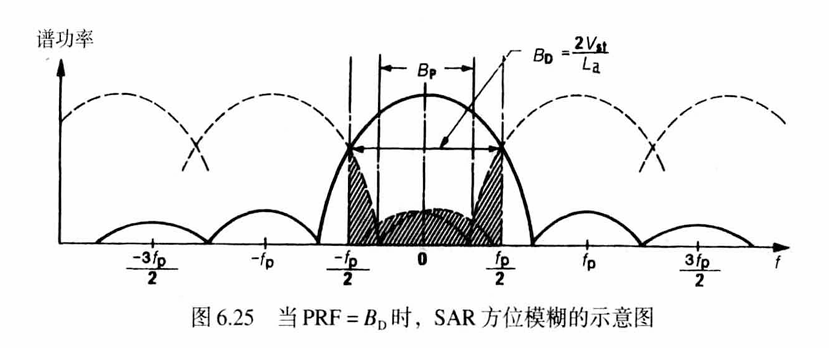
评估方式
方位模糊使用方位模糊比 $AASR$ 评估。
\[AASR \approx \sum_{m=-\infty,m \neq 0}^{+\infty}\frac{\int_{-B_p/2}^{B_p/2}G^2(f+mf_p)df}{\int_{-B_p/2}^{B_p/2}G^2(f)df}\]其中$f$为方位向的多普勒频率, $B_p$为多普勒带宽。
在雷达方程的推导中,已经得到天线增益与 $\theta$, $\lambda$ 存在关系,但不含多普勒频率 $f$。所以需要得到天线增益与多普勒频率的关系。我们知道相对移动会造成多普勒频移,设雷达移动速度为 $v$,斜视角为 $\theta_r$,载波波长为 $\lambda$,则多普勒频率为
天线增益为
\[G = sinc^2(\frac{\pi L_a sin\theta_r}{\lambda})\]$L_a$为方位向天线长度,将 $sin\theta_r$ 与 $\lambda$ 用 $f_d$ 替换,可以得到
\[G = sinc^2(\frac{\pi L_a f_d}{2v})\]PRF 选择
下视角与入射角,地距与斜距
在讨论PRF的选择时,需要先理清下视角与入射角,地距与斜距的关系。
下视角是目标雷达连线与星下点雷达连线的夹角。入射角是斜距与地面法线的夹角,如果是地球为球体,则也是地球半径延长线与斜距的夹角。地距是目标到星下点的距离,斜距是雷达到目标的距离。这样我们可以得到一些关系式。
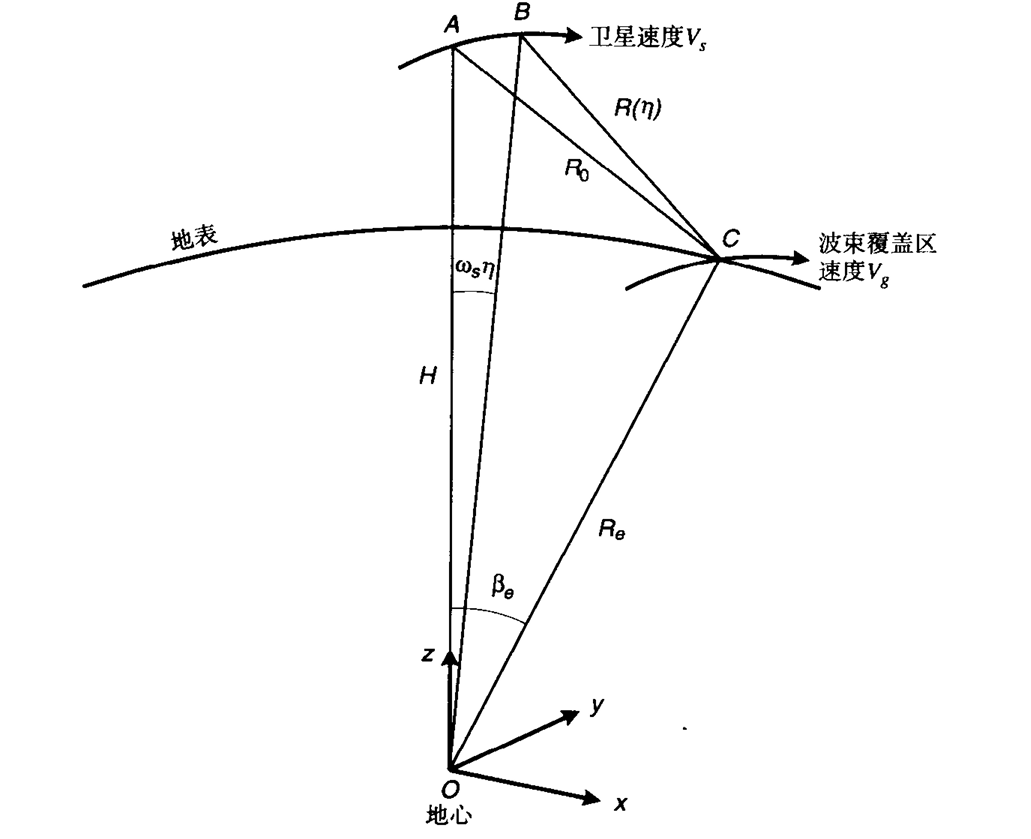
设入射角为 $\eta$,下视角为 $\gamma$,地距对应的张角为 $\beta$,斜距为 $R(\eta)$,地距为 $W$,雷达到地心的距离 $R_s$,目标到地心的距离为 $R_t$。则有
下视角可以由斜距得到
\[\gamma = arccos(\frac{R(\eta)^2+R_s^2-R_t^2}{2R(\eta)R_s})\]斜距,也可以由地距推得
\[\beta = \frac{W}{R_t}\] \[R(\eta) = \sqrt{R_s^2+R_t^2-2R_s^2 R_t^2 cos(\beta)}\]斑马图
较低的PRF会增加方位向频谱的混叠,较高的PRF会减少脉冲间的时间,导致接收回波发生交叠。所以选择一个比较合适的PRF是比较重要的。 首先需要保证的是接收回波与发射脉冲不要发生重叠。如果满足以下条件,则发生干扰
\[T_{emin} = \frac{2R_{min}}{c} = j T_{pri} - \tau - \tau_g,j = 0, \pm 1, \pm 2, \cdots, \pm n\] \[T_{emax} = \frac{2R_{max}}{c} = j T_{pri} + \tau + \tau_g,j = 0, \pm 1, \pm 2, \cdots, \pm n\]而星下点干扰对PRF选择的限制条件为
\[\frac{2H}{c} + jT_{pri} > \frac{2R_{max}}{c},j = 0, \pm 1, \pm 2, \cdots, \pm n\] \[\frac{2H}{c} + jT_{pri} + 2\tau < \frac{2R_{min}}{c},j = 0, \pm 1, \pm 2, \cdots, \pm n\]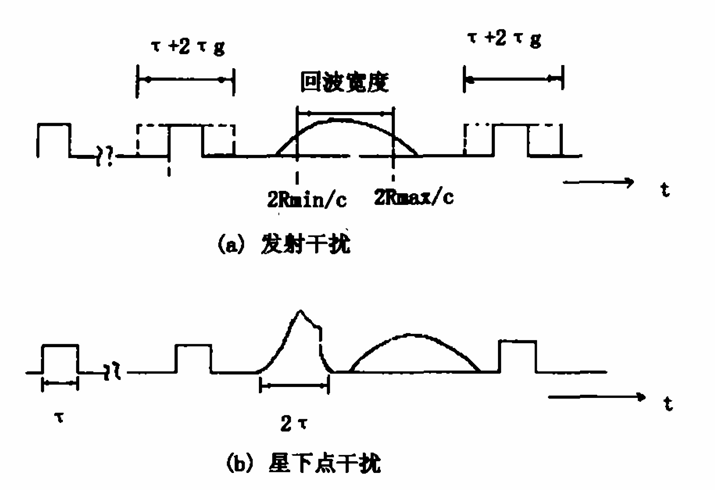
$H$为雷达高度。星下点回波的持续时间不一定为 $2 \tau$ ,它与地形特点有关。