方位向多孔径重建算法表述
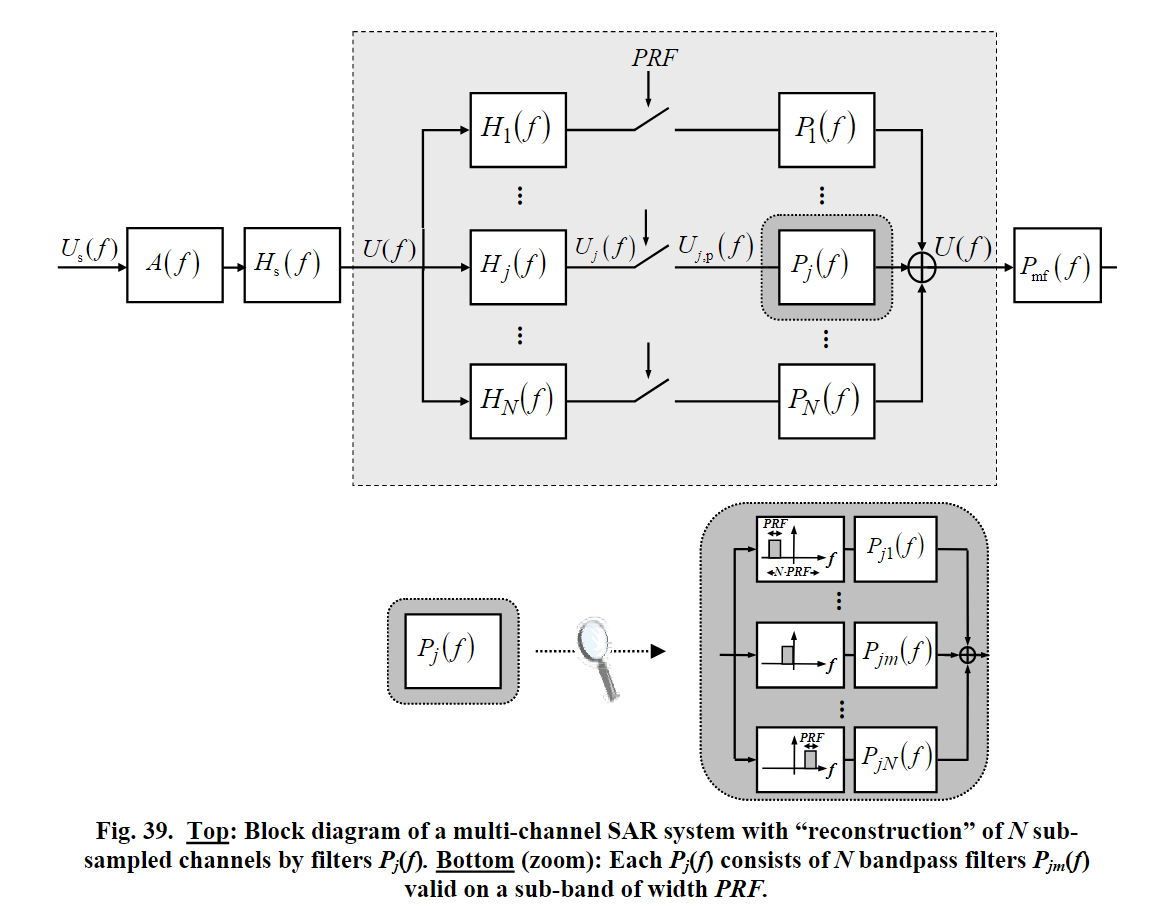
如图,多孔径雷达的信号传输框图,$U_s(f)$ 为发射信号频域。 $A(f),H_s(f)$ 可以简单理解为发射信号所途径的信道的系统响应(发射天线->地面->接收天线)。 $U(f)$ 与传统单孔径收发一体sar雷达所接收的信号一致, $H_j(f)$ 为 对应孔径相较于传统sar雷达所发生的变化,或者说是多孔径系统附加的系统响应,在上一篇中,我们已经分析得到了其解析式。
\[H_j(f) = exp(j \Delta \phi_j) \cdot exp(-j 2\pi f \Delta t_j)\] \[\Delta \phi_j = -\frac{v_g}{v_s}\frac{\pi \Delta x_j^2}{2 \lambda R_0}\] \[\Delta t_j = \frac{\Delta x_j}{2 v_s}\]合并得到
\[H_j(f) = exp(-j \pi \frac{v_g}{v_s}\frac{\Delta x_j^2}{2 \lambda R_0}-j \pi \frac{\Delta x_j}{v_s} f)\]子通道输出信号为 $U_j(f)$,以 $PRF$ 采样率采样得到的信号为 $U_{j,p}(f)$ 。如果想要使用传统sar的聚焦算法,需要将多孔径系统的附加系统响应补偿掉,或者说从 $[U_{1,p}(f) \cdots U_{j,p}(f) \cdots U_{N,p}(f)]$ 中重建出 $U_p(f)$,$U_p(f)$ 为 $U(f)$ 以 $N \cdot PRF$ 采样率采样得到的信号。 由采样定理可以得到,混叠信号 $U_{j,p}$ (只考虑多普勒带宽内的信号)为
\[U_{j,p}(f) = \sum_{n=0}^{N-1}{U_j(f+n \cdot PRF)}=\sum_{n=0}^{N-1}U(f+n \cdot PRF)H_{j}(f+n \cdot PRF)\]写成矩阵形式
\[\bf{U_{jp}} (f) = \bf{U_p}(f) \bf{H}(f)\] \[\bf{U_{jp}} (f) = \begin{bmatrix} U_{1,p}(f) & \cdots & U_{N,p}(f) \end{bmatrix}\] \[\bf{U}(f) = \begin{bmatrix} U(f) & \cdots & U(f+(N-1) \cdot PRF) \end{bmatrix}\] \[\bf{H}(f) = \begin{bmatrix} H_1(f) & \cdots & H_{N}(f)\\ H_1(f + PRF) & \cdots & H_{N}(f + PRF)\\ \vdots & \ddots & \vdots \\ H_1(f + (N-1) \cdot PRF) & \cdots & H_{N}(f + (N-1) \cdot PRF)\\ \end{bmatrix}\]显然,如果 $\bf{H}(f)$ 可逆,则
\[\bf{U}(f) = \bf{U_{jp}}(f) \bf{H^{-1}}(f)\]令 $\bf{P}(f) = \bf{H^{-1}}(f)$,$\bf{P}(f)$ 有如下形式
\[\bf{P}(f) = \begin{bmatrix} P_1(f) & \cdots & P_{1}(f + (N-1) \cdot PRF)\\ P_2(f) & \cdots & P_{2}(f + (N-1) \cdot PRF)\\ \vdots & \ddots & \vdots \\ P_N(f) & \cdots & P_{N}(f + (N-1) \cdot PRF)\\ \end{bmatrix}\]将 $\bf{P}(f)$ 展平就可以得到带宽为 $PRF \cdot N$ 的滤波器了。
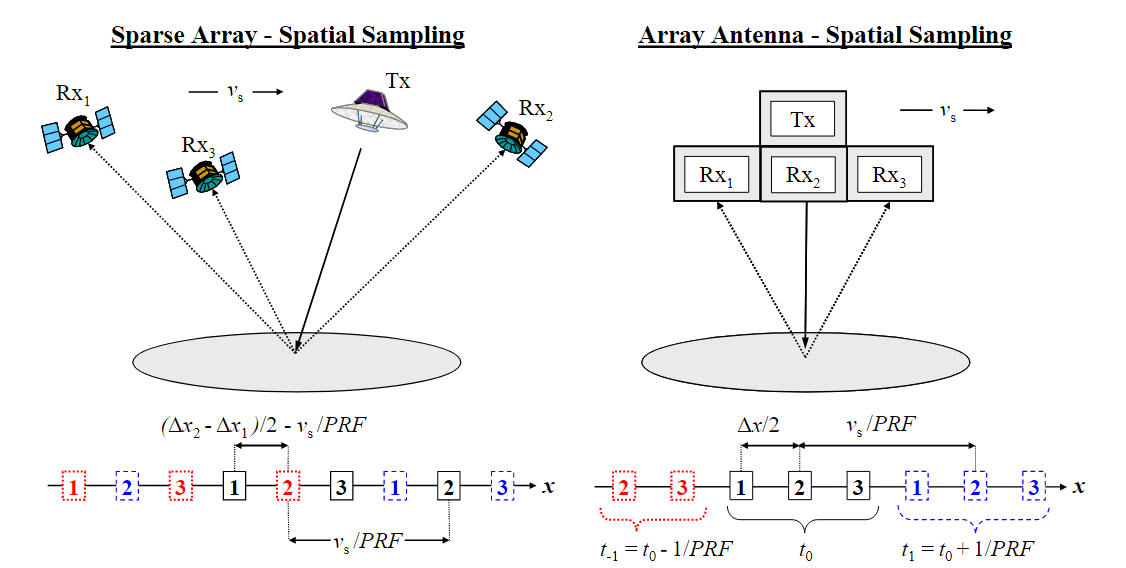
回顾之前讨论系统结构的图,只要各个孔径的采样点排列在方位向信号的不同位置,即使它们没有均匀分布(如果 $PRF = PRF_{uni}$ , 各个孔径的采样点排列后是均匀分布的),我们也能重构出原来的信号。当然,不得不考虑有几个孔径的信号相互重叠,采样了相同时间点,这个时候 $\bf{H}(f)$ 矩阵不再是可逆矩阵,$\bf{P}(f)$ 也就不存在了。
下图为 $N = 2$ 时的示例
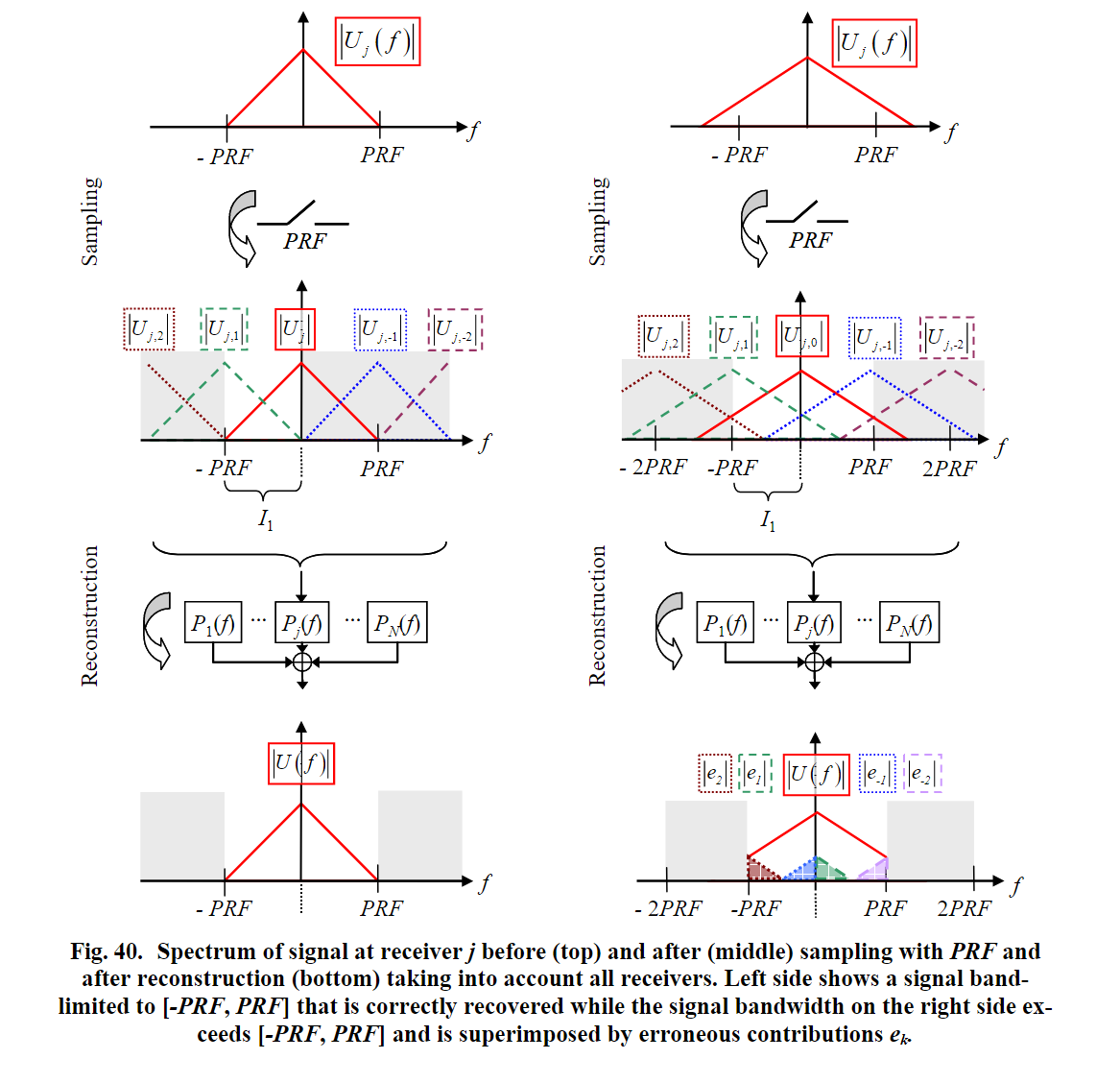
我们再考察一下系统的输出。系统的输出为
\[U_p(f) = \sum_{j=1}^N U_{j,p}(f)P_j(f) \\ = \sum_{j=1}^N \sum_{n=0}^{N-1}U(f+n \cdot PRF)H_{j}(f+n \cdot PRF) P_j(f) \\ = \sum_{n=0}^{N-1}U(f+n \cdot PRF) \sum_{j=1}^N H_{j}(f+n \cdot PRF) P_j(f)\]从上述讨论中,可以看出,该算法无法抑制 频率在 $N \cdot PRF$ 带宽外的信号,与传统sar相似的多普勒模糊依然存在。
算法实现
从 $H_j(f)$ 的解析式中可以发现,$H_j(f)$ 与最短斜距相关,因此 $P_j(f)$ 也与最短斜距相关。所以对于二维sar回波信号来说,每个距离门的重构系数 $\bf{P}(f)$ 不同,我们可能需要逐个进行重建。
同样,也必须考虑距离徙动是否影响重构。根据论文的推算,单平台的多孔径sar无需考虑距离徙动对重构系数的影响。多平台的多孔径sar,不同孔径间的距离徙动需要考虑一个常数项的漂移,这个漂移带来的相位误差就是
\[\Delta \phi_j = -\frac{v_g}{v_s}\frac{\pi \Delta x_j^2}{2 \lambda R_0}\]应该注意到,$\Delta \phi_j$ 与 斜距有关。相应的,重构系数也与斜距有关。但在实际应用中 $\Delta \phi_j$ 对重构系数影响远小于 $\Delta t_j$ 的影响,所以可以忽略。而距离徙动校正需要整个多普勒频谱,所以先进行重构,后进行校正比较好。
算法影响
AASR
这里我们考虑频率距多普勒中心 $N \cdot PRF /2 $ 以上的信号在方位向多孔径雷达中的影响。考虑带外信号 $U_{j,k} = U_j(f+k \cdot PRF)$ , 满足
\[|f| < |\frac{PRF}{2}|\] \[|f+ k \cdot PRF| > \frac{N \cdot PRF}{2}\]第 $j$ 孔径采样后的信号(采样率为 $PRF$)表示为
\[U_{j,p}(f) = \sum_{k=-\infty}^{+\infty} U_j(f+k \cdot PRF) = \sum_{k=-\infty}^{+\infty} U_{j,k}\]考虑到对称性,我们只考虑 $k > 0$ 的情况。
当 $k < \frac{N}{2}$ 时,子带编号为$N-k + 1 \sim N$ 的子带,$|f+ k \cdot PRF|$ 大于 $\frac{N \cdot PRF}{2}$ , ( $-\frac{PRF}{2}$ 开始的子带编号为 $1$), 当 $k > \frac{N}{2}$ 时,所有子带均受到 $U_{j,k}(f)$ 的影响。合并可得到受影响的子带为从 $m_0=max(N-k+1,1) \sim N$ 。 所以第 $j$ 孔径的带外混叠或者说残余混叠可表示为
为了方便,这里
\[H_{jk}(f) = H_j(f+k \cdot PRF)\] \[P_{jm}(f) = P_j(f + m \cdot PRF)\]直接令 $m_0 = 1$ 也可以,重构算法会将非子带($I_m$)内的带内 ($I_n,n \neq m,|n| < N/2$) 信号置为 $0$。对所有孔径与所有 $k$ 求和,可以得到
\[e_{\Sigma}(f) = 2 \sum_{k=1}^{\infty}U_k(f) \cdot \sum_{m=m_0}^{N}\sum_{j=1}^{N}H_{jk}(f) P_{jm}(f)\]由 AASR的定义,我们可以得到
\[AASR_N = \frac{E[|e_\Sigma(f)|^2]}{p_s}\]$p_s$ 为有效信号的功率。
SNR Scaling
这里讨论方位向多孔径系统对SNR的影响。设 $\Phi_{bf}$ 表示 随系统参数的变化,SNR变化的量化因子。设子孔径的输入SNR为 $SNR_{el,j}$,经过重建算法重建后的SNR为 $SNR_{out}$。 $t_r$ 表示快时间(距离向),$t$ 表示慢时间(方位向)。同理 $f_r,f$ 分别表示距离向与方位向的频率。随着系统处理,我们逐步分析信噪比的变化。

信号 $U_j(f_r,f)$ 输入 $j$ 孔径时有一个加性白噪声(包含系统自身的热噪声)$n_{j,B}(t_r,t)$。对应的信号功率为 $p_{s,el,j}$ ,噪声功率为 $p_{n,el,j}$。则 $j$ 孔径的输入信噪比为
\[SNR_{el,j} = \frac{p_{s,el,j}}{p_{n,el,j}} = \frac{p_{tx,av} \cdot E[|U_j(f_r,f) \cdot rect(\frac{f_r}{B})|]}{E[|n_{j,B}(f_r,f) \cdot rect(\frac{f_r}{B})|]}\]这里 $rect(\frac{f_r}{B})$ 表示带通滤波器的影响。后级放大器的增益为 $G_j$,接收机噪声系数为 $F_j$。经过模拟端的放大,孔径 $j$ 的噪声的功率放大到 $G_j \cdot F_j p_{n,el,j}$
之后进行采样,采样会引入量化噪声 $n_{q,j}$。同时由于采样率为 $PRF$,而多孔径信号的有效频段为 $N \cdot PRF$,所以 $N \cdot PRF$ 宽的信号会叠加到一个 $PRF$ 宽的位置里,相当于噪声乘以 $N$,即,$n_j(f)$ 变为 $n_{j,p}(f) = N n_j(f)$ 。再之后,根据之前的讨论,先进行距离压缩与距离徙动校正是比较好的,在此之后,$f_r$ 便不再影响信噪比。
进行重建时,重建算法会把所有孔径的噪声叠加到一起。
\[n(f) = \sum_{j=1}^N P_j(f) \cdot (n_{j,p}(f) \cdot \sqrt{G_j F_j} + n_{q,j}(f))\]对应的噪声功率为
\[p_n(f) = E(|n(f)|^2) = E[|\sum_{j=1}^N P_j(f) \cdot (n_{j,p}(f) \cdot \sqrt{G_j F_j} + n_{q,j}(f))|^2]\]量化噪声 $n_{q,j}(f)$ 与输入噪声 $n_{j,p}(f)$ 是相互独立的,即 $E[n_{q,j}(f)\cdot n_{j,p}(f)] = 0$ 。所以噪声功率可以写为两种噪声功率的和。同理,由于各个孔径是相互独立的,所以累加符号也可以提取出来。
\[p_n = \sum_{j=1}^N E[|n_{j,p}(f) P_j(f)|^2]\cdot G_j F_j + E[|\sum_{j=1}^N P_j(f)n_{q,j}(f)|] = p_{n,rx} + p_{n,q}\]选择合适的系统参数使得量化噪声可以忽略,同时视各个孔径的 $G_j,F_j$ 一致,则我们可以发现,经过系统处理后,噪声放大了
\[G \cdot F \cdot N \sum_{j=1}^N E[|P_j(f)|^2]\]而信号只放大了 $G$ 倍。所以SNR的变化为
\[\frac{SNR_{el}}{SNR_{out}} = F \cdot N \sum_{j=1}^N E[|P_j(f)|^2]\]对其进行标准化,考虑 $PRF = PRF_{uni}$ 的时候。此时无需重构滤波器也可以进行聚焦,整个系统处理与传统的sar雷达系统相似,将此时作为标准,
\[\frac{SNR_{el}}{SNR_{out}}|_{uni} = F\]标准化后,得到
\[\Phi_{bf}(PRF) = \frac{SNR_{el}}{SNR_{out}} / \frac{SNR_{el}}{SNR_{out}}|_{uni} = N \sum_{j=1}^N E[|P_j(f)|^2]\]NESZ
设发射功率为 $P_{tx}$,波长为 $\lambda$,斜距为 $R(\theta_i)$。目标后向散射截面积为 $\sigma$,天线增益为 $G_{rx,j}(\theta_{az}, \theta_i)$,$G_{tx}(\theta_{az}, \theta_i)$。$L$ 表示所有的功率损失。等效的噪声功率为 $kT_0BF$,$k$ 为玻尔兹曼常数,$T_0$ 为等效温度,$B$ 为系统带宽,$F$ 为接收机噪声系数,方位向的功率损失为 $L_{az}$。由雷达方程可以得到单一孔径的SNR
\[SNR_0 = \frac{P_{tx} G_{tx}(\theta_{az}, \theta_i) G_{rx,j}(\theta_{az}, \theta_i) \lambda^2 }{(4 \pi) (4\pi R(\theta_i)^2)^2 \cdot L \cdot kT_0BF L_{az}} \sigma\]经过脉冲压缩处理后,$SNR$ 扩大 $N_{rg} N_{az}$ 倍。$N_{rg},N_{az}$ 分别为方位向和距离向的脉冲压缩比。目标照射时间为 $T_{az}$,距离向与方位向的分辨率为 $\delta_{rg},\delta_{az}$ 。
\[SNR_1 = N_{az}N_{rg}SNR_0\] \[N_{rg} = B\tau\] \[N_{az} = T_{az} PRF = \frac{R(\theta_i) \lambda}{d_{rx,az} \cdot v_s} PRF = \frac{R(\theta_i) \lambda}{2 \delta_{az} v_s}\]设每个目标的后向散射系数都等于 $\sigma_0$ ,则
\[\sigma = \delta_{az} \delta_{rg} \sigma_0\]经过重构算法后,如果未按 $PRF_{uni} 采样,$由上一节讨论可得,还需要乘以一个系数 $\Phi_{bf}$ 。同时 $N$ 个孔径的叠加也会将信噪比扩大 $N$ 倍。
\[SNR_2 = N\Phi_{bf} SNR_1\]最终得到 $NESZ$ 为
\[NESZ =\frac{\sigma_0}{SNR} =\frac{256 \pi^3 R(\theta_i)^3 v_s \sin(\theta_i) k T_0 B F\Phi_{bf} L \cdot L_{az}}{P_{tx} G_{tx}(\theta_{az}, \theta_i) G_{rx,j}(\theta_{az}, \theta_i) \lambda^3 N c PRF \tau}\]