方位向多孔径雷达的作用
孔径大小不变，增加孔径数量能够间接提高等效PRF，则系统可分析的多普勒带宽得到了提高。
\[B_{az} \leq N \cdot PRF\]多普勒带宽提高，所对应的方位向分辨率也就得到提高。
\[\delta_{az} \approx \frac{Vs}{B_{az}}\]方位向多孔径雷达的系统响应
相对于单孔径雷达的收发一体，多孔径雷达的TX/RX是分开的，信号的发射路径于接收路径不一定相同（接收天线与发射天线不一定相同，甚至不一定为同一个卫星）。
对于给定的一个接收天线 $i$ ，其与发射天线的距离为 $\Delta x_i$。则方位向的接收信号为
显然，与单孔径接收信号对比，多孔径的接收信号不再是简单的 $2 R(t)$ ，需要对发送与接收分别考虑。其中，如果 $\Delta x_i$ 足够小，接收路径可表示为
\[R_i(t) = R(t-\frac{\Delta x_i}{v_s})\]使用斜距的近似表达式
\[R(t) \approx R_0 + \frac{v_g v_s}{2 R_0} t^2\]代入到接收信号中，可以化简得到
\[h_i(t) \approx exp(-j \frac{4 \pi}{\lambda}R_0) \cdot exp(-j \frac{v_g}{v_s}\frac{\pi \Delta x_i^2}{2 \lambda R_0}) \cdot exp[-j \frac{2\pi v_g v_s}{\lambda}\frac{(t-\frac{\Delta x_i}{2 v_s})^2}{R_0}]\]可以看出，相较于单孔径的接收信号，多孔径中某一孔径的接收信号多出了一个相偏
\[\Delta \phi_i = -\frac{v_g}{v_s}\frac{\pi \Delta x_i^2}{2 \lambda R_0}\]与一个时延
\[\Delta t_i = \frac{\Delta x_i}{2 v_s}\]这些在频域上可简化为一个因子，也就是一个滤波器
\[H_i(f) = exp(j \Delta \phi_i) \cdot exp(-j 2\pi f \Delta t_i)\]接收与发射的空间关系
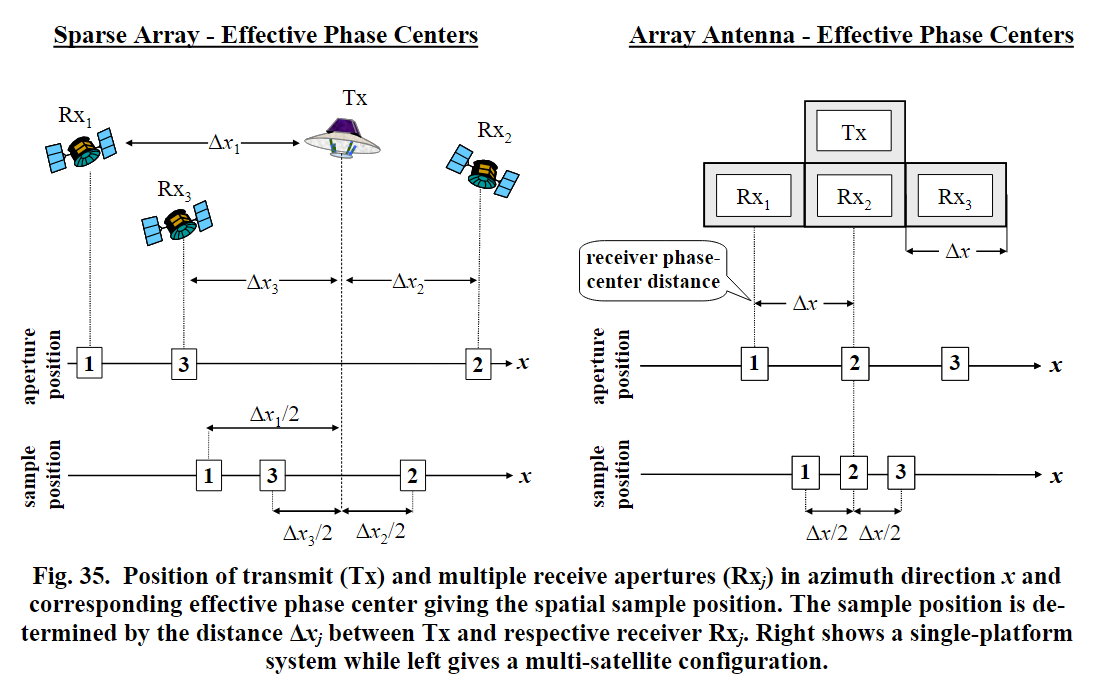
由上一节的分析可以知道，发射孔径与接收孔径的空间距离 $\Delta x$ 会导致在采样中有一个时延 $\Delta t = \frac{\Delta x}{v_s}$，换算到距离，相当于采样空间中有一个距离 $\Delta x / 2$。如果想要各个孔径的接收数据在采样空间中，按照雷达移动的方式排列，就必须满足一定关系。
换句话说，就是想要对于相邻的两个接收孔径中，其接收的数据也是邻接的。且任意两个相邻的孔径，其采样的邻接距离相等。为什么要这样？因为对于单孔径的雷达，它是匀速移动的。如果想使用单孔径雷达的算法，也要让多个孔径的数据在组合在一起后也有一个雷达匀速移动的效果，前面孔径对应前面的地形，后面的孔径对应后面的地形，且照射面等距排列。或者说，如果不这样，那多孔径对应的雷达移动不再匀速移动，会产生一定的畸变，一会儿快，一会儿慢。
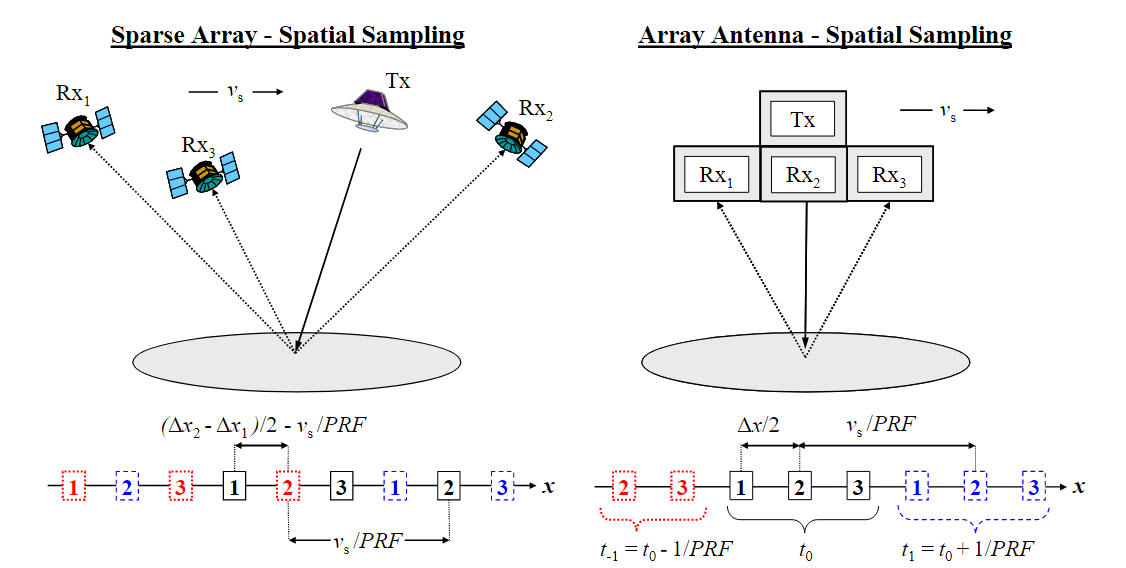
当然，如图所示，数据不需要按照发射时间进行排列。我们是否可以找到一个PRF，让不同孔径的数据相互排列，从而达到线性排列的效果？设孔径 $j$ ，参考孔径 $1$ 与发射孔径的距离为 $\Delta x_j$， $\Delta x_1$。则在采样空间中，两个孔径对于一个发射信号所采样到的数据间的距离为
\[\Delta x_s = \frac{\Delta x_j - \Delta x_i}{2}\]如果是多卫星，两个接收孔径的到达时延可能相差好几个 PRI，此时他们对应的邻接数据为
\[\Delta x_s = \frac{\Delta x_j - \Delta x_i}{2} - \frac{k v_s}{PRF}\]我们希望数据排列按照单孔径雷达匀速移动采样到的数据排列的效果一致，也就是将 $\frac{v_s}{PRF}$等分成N份，孔径 $1$ 采第一份，孔径 $2$ 采第二份，孔径 $j$ 采第 $j$ 份
\[\Delta x_s = \frac{\Delta x_j - \Delta x_1}{2} - \frac{kv_s}{PRF} = (j-1)\frac{v_s}{N \cdot PRF}\]可以得到
\[\Delta x_j - \Delta x_1 = \frac{2 v_s}{PRF}(\frac{j-1}{N} + k)\]如果系统是单平台，即使用阵列天线实现多孔径，则
\[k = 0\]孔径间的距离为
\[\Delta x = \frac{2 v_s}{N \cdot PRF}\]或者说，多孔径与单孔径的数据模式保持一致的PRF为
\[PRF_{uni} = \frac{2v_s}{N\Delta x} = \frac{2 v_s}{l_{az}}\]当然
\[PRF_{uni,k} = k \cdot PRF_{uni}\]也满足要求，但要满足
\[k \neq \frac{p N}{m} \enspace m \in {1,m,\cdots,N}; p,N \in \mathbb{N}\]