背景
DBF技术旨在解决随着成像带的扩大,雷达成像性能下降的问题。对于传统的单通道SAR系统,更宽的测绘带意味着更宽的天线波束,而更宽的接收波束意味着更小的天线孔径,而天线孔径的减小会导致天线增益的下降,从而是SNR降低,成像性能恶化。DBF主要通过在接收端使用多个通道,将不同的通道进行加权,在不同的快时间对不同的斜距范围进行高增益的扫描,从而实现宽测绘,高增益。
系统几何

如图所示,设不同通道间的距离为 $d_{ra}$ , 则第 $n$ 个通道接收信号为
\(r_n(t) = rect[\frac{t-t_n}{T_p}] exp[j \pi K_r(t-t_n)^2]exp[-j2 \pi f_c t_n]\) 其中 $T_p$ 为脉冲宽度,$f_c$ 为载波频率。$K_r$ 为距离向调频率 $ t_n = t_{ref} - \Delta t_n$ 为当前通道的时延,其中
\[\Delta t_n = \frac{d_n \sin(\theta(t_{ref}) - \beta)}{c}\]$d_n$ 为通道 $n$ 相较于参考通道的距离,$\theta(t_{ref})$ 为在 $t_{ref}$ 时间到达的回波对应的目标的下视角,$\beta$ 为当前天线安装角,不同波位可能不同, $c$ 为光速。可以认为 $\Delta t_n « t_{ref}$。所以展开 $r_n(t)$ , 将相位中 $\Delta t_n$ 作为因子的项忽略, 则可以得到
\[r_n(t) = rect[\frac{t-t_n}{T_p}] exp[j \pi K_r(t-t_{ref})^2]exp[-j2 \pi f_c t_{n}] = r_{ref}(t) exp[j2 \pi f_c \Delta t_{n}]\]类似于阵列天线。
处理模型
如上所诉,如果简单将各个通道的信号加起来,则其表现与阵列天线并无本质不同,也不满足宽幅要求。所以各个通道的信号还需做一定处理才能合并。

如图所示,相较于简单地加在一起,这种模型对每个通道地信号进行加权处理。加权因子该怎样选取呢,可以先观察没有加权时的合并输出。将 $\Delta t_n$ 展开
\[r_n(t) = r_{ref}(t) exp[j2 \pi \frac{d_n \sin(\theta(t_{ref}) - \beta)}{\lambda}]\]其中 $\lambda = f_c / c$ 对各个通道进行求和,将相位中心通道作为参考通道,令 $\theta(t_{ref}) = \theta_{ref}$ 有
\[r_{sum} = r_{ref}(t) \frac{\sin[\pi N_r d_{ra}(\sin(\theta_{ref} - \beta))]}{\sin[\pi d_{ra}(\sin(\theta_{ref} - \beta))]}\]其中 $N_r$ 为通道数量。$d_{ra}$ 为相邻通道的间隔。可以观察到幅度大小与附加相位有关,即 $\Delta t_n$,如果我们将每个通道都乘以 $\omega_i (t)$ ,其中 $\omega_i (t)$ 满足
\[\omega_i(t) = exp(-j 2 \pi f_c \Delta t_n) = exp[-j2 \pi \frac{d_n \sin(\theta(t_{ref}) - \beta)}{\lambda}]\]则新的合并信号为
\[r_{sum} = N_r \cdot r_{ref}(t)\]满足提高接收信号幅度大小的要求。对于不同斜距的目标,由于回波到达时间不同,在不同的回波到达时间使用不同的加权因子,就能放大对应目标了。但如果加权因子不能实时对应,则合成出来的信号会存在明显栅瓣,同时主瓣展宽。
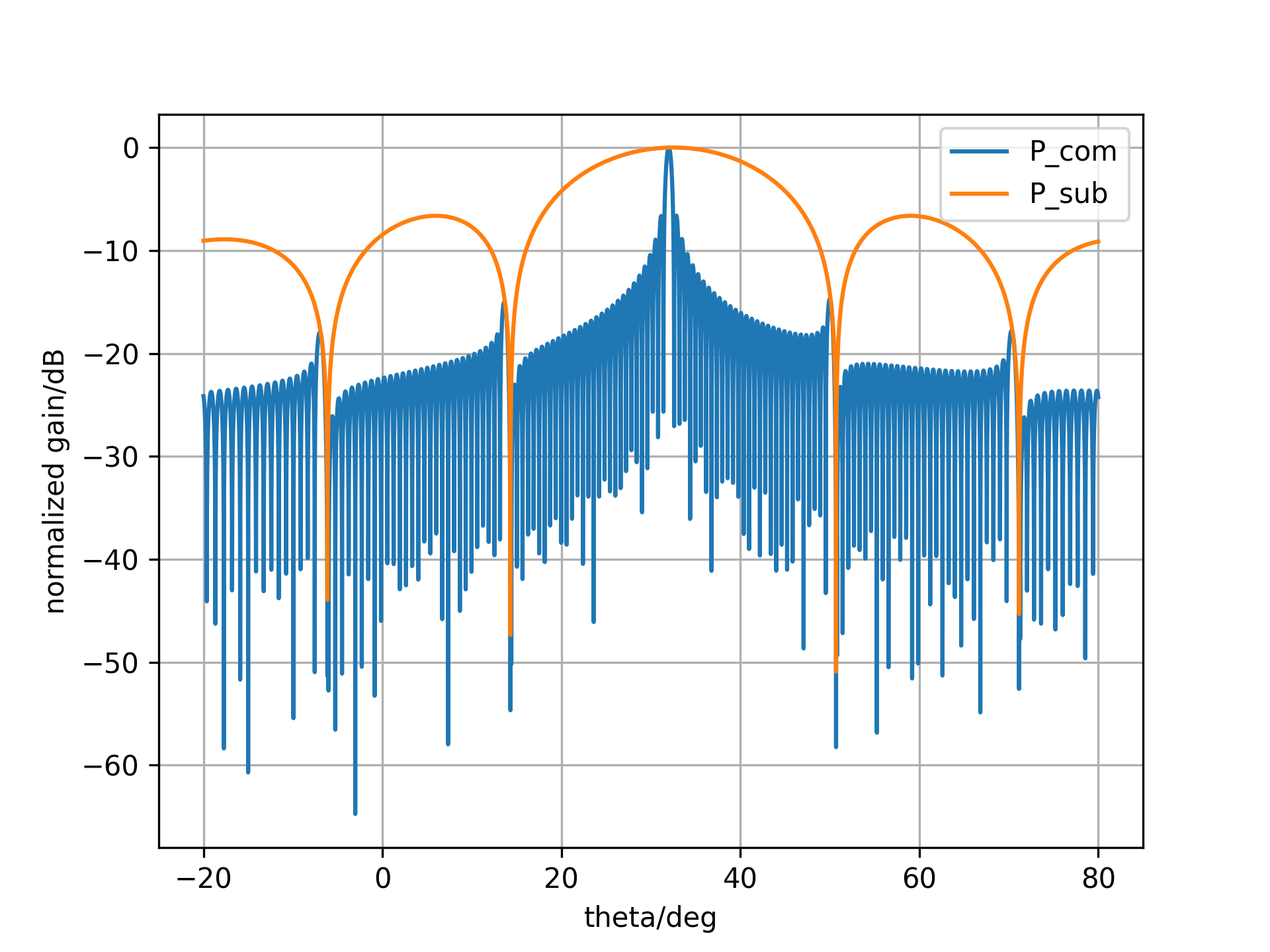
由于脉冲存在一定宽度,所以这种实时对应是很难做到的,其接收增益降低,主瓣展开。通常叫做为脉冲延展损失。克服这个损失的方法有很多种,但考虑到合成需要星上进行,所以其处理复杂度越少越好。其中FIR时延滤波处理比较实用。

如图所示,在加权后,将每个通道进行延时,其第 $i$ 个通道的延时系统函数为
\(H_{fir,i} = exp(j2\pi \frac{(i-1)\alpha}{K_r} f)\) \(\alpha = \frac{d_i}{\lambda} \frac{\partial \theta(t_{ref})}{\partial t_{ref}} |_{t_{ref} = t_c}\)
其中 $t_c$ 为场景中心时延。其主要假设在于 $theta(t_{ref})$ 相较于 $t_{ref}$ 近似线性变化。
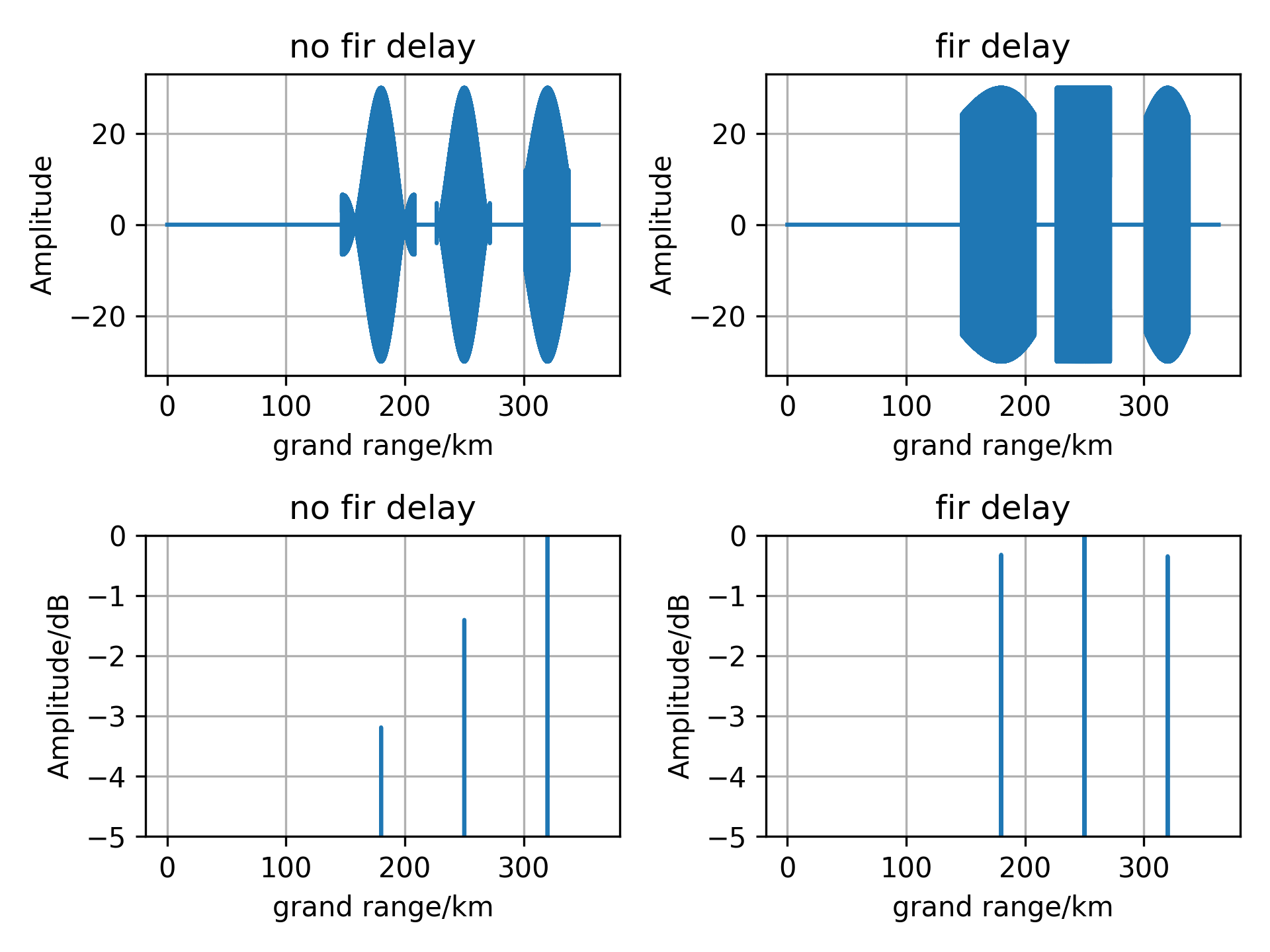
可以看出FIR时延滤波效果比较好,但其主要假设满足条件比较苛刻,对偏导值的大小选取比较敏感。对于主瓣展开问题,也有相应算法的提出。其中有一个与CSA算法比较类似。通过对各个通道间的主误差时延与残余误差时延进行补偿,将各个通道与接收回波匹配。其中第 $n$ 个通道的主误差补偿时延为
\[D_n = \frac{d_n \sin(\theta_c - \beta)}{c}\]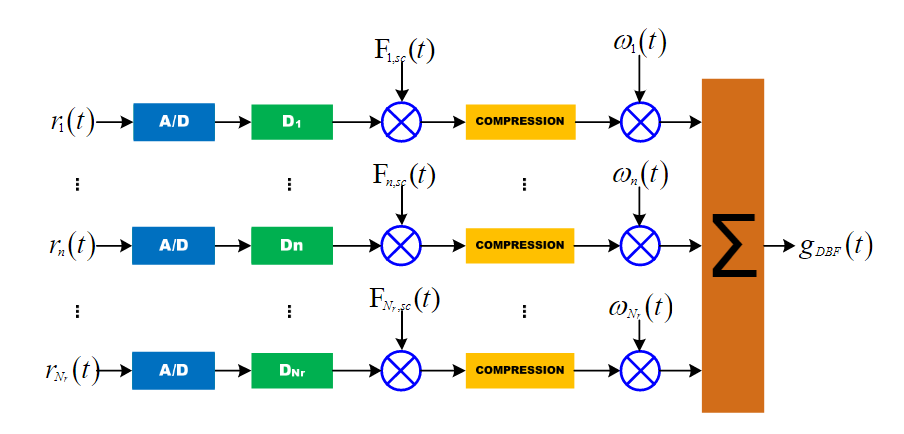
其中 $\theta_c$ 为场景中心下视角。残余误差时延补偿通过在距离压缩后通过变标方程解决。第 $n$ 个通道的变标方程为
\[F_{n,sc}(t) = exp[-j \pi K_r \frac{d_n}{c} (\frac{\partial sin(\theta(t)-\beta)}{\partial t} |_{t = t_c})(t-t_c)^2]\]其中 $\theta(t)$ 为参考通道对应下视角随快时间的变化。其主要假设也在于认为 $sin(\theta(t)-\beta)$ 为线性的,该假设也比较苛刻。同时需要去除FIR时延处理
可以看出,虽然主瓣展宽有很大改善,但峰值旁瓣比恶化。